《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

10. 在同一平面直角坐标系中,有下列函数图象：①$y= x^{2}$.②$y= -\frac{1}{2}x^{2}$.③$y= 3x^{2}$.④$y= -x^{2}$,其中开口最小的是(B)
A.④
B.③
C.②
D.①

答案： B

11. 已知二次函数$y= \frac{1}{4}x^{2}$,则它的图象上到x轴、y轴距离相等的点有(4,4),(-4,4),(0,0).

答案： (4,4),(-4,4),(0,0)

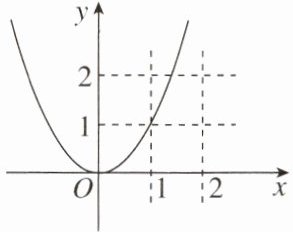
12. 如图,若抛物线$y= ax^{2}(a\neq0)与四条直线x= 1$,$x= 2$,$y= 1$,$y= 2$围成的正方形有公共点(包括边界及顶点),则a的取值范围为1/4≤a≤2.

答案： 1/4≤a≤2

13. 已知二次函数$y= ax^{2}(a\neq0)的图象过点(1,\frac{3}{2})$,有下列点：$(-1,\frac{3}{2})$,$(1,-\frac{3}{2})$,$(2,6)$,$(\sqrt{2},3)$.其中哪些点在图象上？请说明理由.

答案： 解:由题知,将点(1,3/2)的坐标代入二次函数表达式得,
a×1²=3/2,解得a=3/2.
所以二次函数的表达式为y=3/2x².
将x=-1代入二次函数表达式得,
y=3/2×(-1)²=3/2,所以点(-1,3/2)在函数图象上;
将x=1代入二次函数表达式得,
y=3/2×1²=3/2≠-3/2,所以点(1,-3/2)不在函数图象上;
将x=2代入二次函数表达式得,
y=3/2×2²=6,所以点(2,6)在函数图象上;
将x=√2代入二次函数表达式得,
y=3/2×(√2)²=3,所以点(√2,3)在函数图象上.
综上所述,点(-1,3/2),(2,6),(√2,3)在二次函数y=3/2x²的图象上.

14. 已知二次函数$y= ax^{2}的图象经过点A(-1,-\frac{1}{2})$.
(1)求这个二次函数的表达式.
(2)请写出这个二次函数图象的顶点坐标、对称轴和开口方向.

答案：
(1)
∵二次函数y=ax²的图象经过A(-1,-1/2),
∴-1/2=a×(-1)²,解得a=-1/2,
∴二次函数的表达式为y=-1/2x².
(2)
∵二次函数的表达式为y=-1/2x²,
∴这个二次函数图象的顶点坐标为(0,0),对称轴为y轴,开口向下.