《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

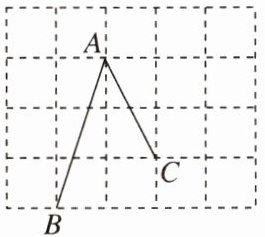
10. 如图,在4×5的正方形网格中,A,B,C为格点(小正方形的顶点),则$\sin A = \underline{$\frac{\sqrt{2}}{2}$}$

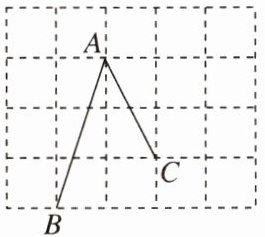
答案： $\frac{\sqrt{2}}{2}$

11. 已知$\alpha$为锐角,若$\sqrt{3}\tan^2 \alpha - 4\tan \alpha + \sqrt{3} = 0$,则$\alpha的度数为\underline{$60^{\circ}$或$30^{\circ}$}$

答案： $60^{\circ}$或$30^{\circ}$

12. 小明的一道错题如下所示,请仔细观察并解决以下问题：
$6\sin 60° - 3\tan 45° + \sqrt{9}$
$= 6 × \frac{\sqrt{3}}{3} - 3 × 3\sqrt{3} + 3…①$
$= 2\sqrt{3} - 3\sqrt{3} + 3…②$
$= -\sqrt{3} + 3…③$
(1)错误步骤：$\underline{①}$(填最先出错的步骤序号即可)
(2)写出正确的解答步骤。
解：原式$=6× \frac{\sqrt{3}}{2}-3× 1+3=3\sqrt{3}-3+3=3\sqrt{3}$

答案： 解:
(1)$\because \sin 60^{\circ}=\frac{\sqrt{3}}{2}$,$\tan 45^{\circ}=1$,
$\therefore$第①步出现错误.
故答案为①.
(2)原式$=6× \frac{\sqrt{3}}{2}-3× 1+3=3\sqrt{3}-3+3=3\sqrt{3}$.

13. 对于钝角$\alpha$,定义它的三角函数值如下：
$\sin \alpha = \sin(180^\circ - \alpha)$,$\cos \alpha = -\cos(180^\circ - \alpha)$。
(1)求$\sin 120^\circ$,$\cos 120^\circ$,$\sin 150^\circ$的值。
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,$\sin A$,$\cos B是方程4x^2 - mx - 1 = 0$的两个不相等的实数根,求m的值及$\angle A和\angle B$的大小。

答案： 解:
(1)由题意得,
$\sin 120^{\circ}=\sin(180^{\circ}-120^{\circ})=\sin 60^{\circ}=\frac{\sqrt{3}}{2}$,
$\cos 120^{\circ}=-\cos(180^{\circ}-120^{\circ})=-\cos 60^{\circ}=-\frac{1}{2}$,
$\sin 150^{\circ}=\sin(180^{\circ}-150^{\circ})=\sin 30^{\circ}=\frac{1}{2}$.
(2)$\because$三角形的三个内角的比是$1:1:4$,
$\therefore$三个内角分别为$30^{\circ}$,$30^{\circ}$,$120^{\circ}$.
①当$\angle A=30^{\circ}$,$\angle B=120^{\circ}$时,方程的两根为$\frac{1}{2}$,
$-\frac{1}{2}$.
将$x=\frac{1}{2}$代入方程得$4× \left( \frac{1}{2}\right)^{2}-m× \frac{1}{2}-1=0$,
解得$m=0$,
经检验$x=-\frac{1}{2}$是方程$4x^{2}-1=0$的根,
$\therefore m=0$符合题意;
②当$\angle A=120^{\circ}$,$\angle B=30^{\circ}$时,两根为$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$,不符合题意;
③当$\angle A=30^{\circ}$,$\angle B=30^{\circ}$时,两根为$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,
将$x=\frac{1}{2}$代入方程得$4× \left( \frac{1}{2}\right)^{2}-m× \frac{1}{2}-1=0$,
解得$m=0$,
经检验$x=\frac{\sqrt{3}}{2}$不是方程$4x^{2}-1=0$的根.
综上所述,$m=0$,$\angle A=30^{\circ}$,$\angle B=120^{\circ}$.