第51页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
9. 如图,AD 与 BC 相交于点 O,∠A= ∠C,AO= 4,CO= 2,AB= 6,求 CD 的长.


答案:
解:
∵∠A=∠C,∠AOB=∠COD,
∴△AOB∽△COD,
∴$\frac{AB}{CD}=\frac{OA}{OC}$,即$\frac{6}{CD}=\frac{4}{2}$,
解得CD=3,即CD的长为3.
∵∠A=∠C,∠AOB=∠COD,
∴△AOB∽△COD,
∴$\frac{AB}{CD}=\frac{OA}{OC}$,即$\frac{6}{CD}=\frac{4}{2}$,
解得CD=3,即CD的长为3.
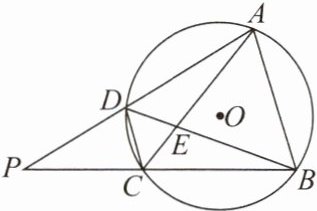
10. 如图,⊙O 的内接四边形 ABCD 的一组对边 AD 和 BC 延长后相交于点 P,对角线 AC 和 BD 相交于点 E,则图中共有相似三角形(
A.1 对
B.2 对
C.3 对
D.4 对
D
)
A.1 对
B.2 对
C.3 对
D.4 对
答案:
D【解析】
∵∠DAE=∠CBE,∠BCE=∠ADE,
∴△DAE∽△CBE,同理可得,△DCE∽△ABE.
∵四边形ABCD是⊙O的内接四边形,
∴∠PDC=∠PBA,∠PCD=∠PAB,
∴△PCD∽△PAB.
∵∠DPB=∠CPA,∠PBD=∠PAC,
∴△PBD∽△PAC.
综上,共有4对相似三角形.
∵∠DAE=∠CBE,∠BCE=∠ADE,
∴△DAE∽△CBE,同理可得,△DCE∽△ABE.
∵四边形ABCD是⊙O的内接四边形,
∴∠PDC=∠PBA,∠PCD=∠PAB,
∴△PCD∽△PAB.
∵∠DPB=∠CPA,∠PBD=∠PAC,
∴△PBD∽△PAC.
综上,共有4对相似三角形.
11. 已知在平行四边形 ABCD 中,点 E 在直线 AD 上,AE= $\frac{1}{3}$AD,连结 CE 交 BD 于点 F,则 EF:FC 的值是______.
答案:
$\frac{2}{3}$或$\frac{4}{3}$【解析】
∵AE=$\frac{1}{3}$AD,
∴分两种情况:
①当点E在线段AD上时,如图1所示.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DEF=∠BCF,∠EDF=∠CBF,
∴△EFD∽△CFB,
∴EF:FC=DE:BC.
∵AE=$\frac{1}{3}$AD,
∴DE=2AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,
∴DE:BC=2:3,
∴EF:FC=2:3.
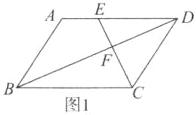
②当点E在线段DA的延长线上时,如图2所示.
同①得△EFD∽△CFB,
∴EF:FC=DE:BC.
∵AE=$\frac{1}{3}$AD,
∴DE=4AE=$\frac{4}{3}$AD=$\frac{4}{3}$BC,
∴DE:BC=4:3,
∴EF:FC=4:3.
综上所述,EF:FC的值是$\frac{2}{3}$或$\frac{4}{3}$.

$\frac{2}{3}$或$\frac{4}{3}$【解析】
∵AE=$\frac{1}{3}$AD,
∴分两种情况:
①当点E在线段AD上时,如图1所示.
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DEF=∠BCF,∠EDF=∠CBF,
∴△EFD∽△CFB,
∴EF:FC=DE:BC.
∵AE=$\frac{1}{3}$AD,
∴DE=2AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,
∴DE:BC=2:3,
∴EF:FC=2:3.

②当点E在线段DA的延长线上时,如图2所示.
同①得△EFD∽△CFB,
∴EF:FC=DE:BC.
∵AE=$\frac{1}{3}$AD,
∴DE=4AE=$\frac{4}{3}$AD=$\frac{4}{3}$BC,
∴DE:BC=4:3,
∴EF:FC=4:3.
综上所述,EF:FC的值是$\frac{2}{3}$或$\frac{4}{3}$.

12. 如图,四边形 ABCD 是正方形,点 G 为边 CD 上一点,连结 AG 并延长,交 BC 的延长线于点 F,连结 BD 交 AF 于点 E,连结 EC. 求证:
(1)∠DAE= ∠DCE.
(2)△EGC∽△ECF.
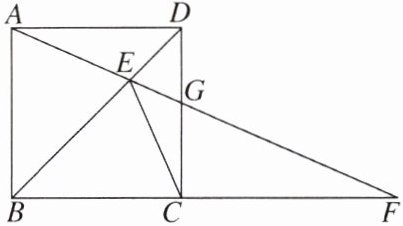
(1)∠DAE= ∠DCE.
(2)△EGC∽△ECF.

答案:
证明:
(1)
∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠CDE=45°,AD//BC.
在△ADE和△CDE中,
$\left\{\begin{array}{l}AD=CD,\\ \angle ADE=\angle CDE,\\ DE=DE,\end{array}\right.$
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE.
(2)
∵AD//CF,
∴∠DAE=∠F,
∴∠DCE=∠F.
又
∵∠CEG=∠FEC,
∴△EGC∽△ECF.
(1)
∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠CDE=45°,AD//BC.
在△ADE和△CDE中,
$\left\{\begin{array}{l}AD=CD,\\ \angle ADE=\angle CDE,\\ DE=DE,\end{array}\right.$
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE.
(2)
∵AD//CF,
∴∠DAE=∠F,
∴∠DCE=∠F.
又
∵∠CEG=∠FEC,
∴△EGC∽△ECF.
13. 如图,在矩形 ABCD 中,E 是 BC 的中点,DF⊥AE,垂足为 F.
(1)求证:△ABE∽△DFA.
(2)若 AB= 6,BC= 4,求 DF 的长.

(1)求证:△ABE∽△DFA.
(2)若 AB= 6,BC= 4,求 DF 的长.

答案:
解:
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA.
(2)
∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE=$\sqrt{AB^2+BE^2}=\sqrt{6^2+2^2}=2\sqrt{10}$.
∵四边形ABCD是矩形,
∴AD=BC=4.
∵△ABE∽△DFA,
∴$\frac{AB}{DF}=\frac{AE}{AD}$,
∴DF=$\frac{AB\cdot AD}{AE}=\frac{6×4}{2\sqrt{10}}=\frac{6}{5}\sqrt{10}$.
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA.
(2)
∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE=$\sqrt{AB^2+BE^2}=\sqrt{6^2+2^2}=2\sqrt{10}$.
∵四边形ABCD是矩形,
∴AD=BC=4.
∵△ABE∽△DFA,
∴$\frac{AB}{DF}=\frac{AE}{AD}$,
∴DF=$\frac{AB\cdot AD}{AE}=\frac{6×4}{2\sqrt{10}}=\frac{6}{5}\sqrt{10}$.
查看更多完整答案,请扫码查看


