第33页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
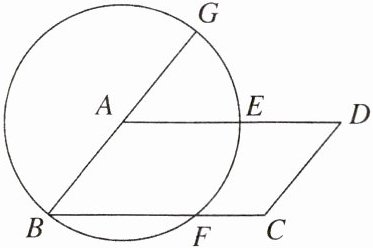
9. 如图,以平行四边形ABCD的顶点A为圆心,AB为半径作⊙A,分别交AD,BC于点E,F,延长BA交⊙A于点G,求证:$\overset{\frown}{GE}= \overset{\frown}{EF}$.

答案:
证明:如图,连结AF,$\because AB=AF$,$\therefore \angle ABF=\angle AFB$.$\because$四边形ABCD是平行四边形,$\therefore AD// BC$,$\therefore \angle DAF=\angle AFB$,$\angle GAE=\angle ABF$,$\therefore \angle GAE=\angle EAF$,$\therefore GE=EF$.
证明:如图,连结AF,$\because AB=AF$,$\therefore \angle ABF=\angle AFB$.$\because$四边形ABCD是平行四边形,$\therefore AD// BC$,$\therefore \angle DAF=\angle AFB$,$\angle GAE=\angle ABF$,$\therefore \angle GAE=\angle EAF$,$\therefore GE=EF$.

10. 如图,C是⊙O直径AB上的一点,过点C作弦DE,使CD= CO,若$\overset{\frown}{AD}$所对圆心角的度数为40°,则$\overset{\frown}{BE}$所对圆心角的度数为(
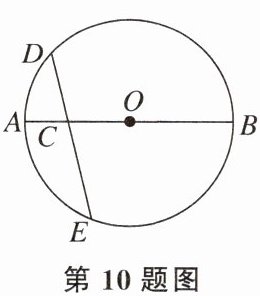
A.40°
B.80°
C.150°
D.120°
D
)
A.40°
B.80°
C.150°
D.120°
答案:
D
11. 已知⊙O的半径为2,△ABC内接于⊙O,$\overset{\frown}{AB}$,$\overset{\frown}{BC}$,$\overset{\frown}{AC}$的长之比为3∶2∶3,则BC的长为
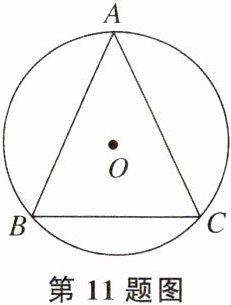
$2\sqrt{2}$
.
答案:
$2\sqrt{2}$
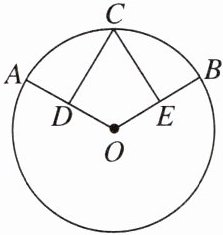
12. 如图,点C在⊙O上,CD⊥OA于点D,CE⊥OB于点E,OD= OE. 求证:C是$\overset{\frown}{AB}$的中点.

答案:
证明:如图,连结OC.$\because CD\perp OA$于点D,CE$\perp OB$于点E,$\therefore \angle CDO=\angle CEO=90^\circ$.$\because OC=OC$,$OD=OE$,$\therefore \triangle COD\cong \triangle COE(HL)$,$\therefore \angle AOC=\angle BOC$,$\therefore \overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore$C是$\overset{\frown}{AB}$的中点.
证明:如图,连结OC.$\because CD\perp OA$于点D,CE$\perp OB$于点E,$\therefore \angle CDO=\angle CEO=90^\circ$.$\because OC=OC$,$OD=OE$,$\therefore \triangle COD\cong \triangle COE(HL)$,$\therefore \angle AOC=\angle BOC$,$\therefore \overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore$C是$\overset{\frown}{AB}$的中点.

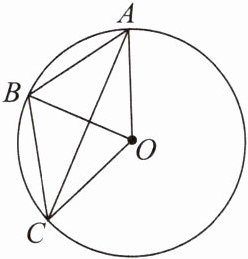
13. 如图,AB,BC,AC都是⊙O的弦,且∠AOB= ∠BOC. 求证:(1)∠BAC= ∠BCA. (2)∠ABO= ∠CBO.

答案:
证明:
(1)$\because \angle AOB=\angle BOC$,$\therefore \overset{\frown}{AB}=\overset{\frown}{BC}$,$BA=BC$,$\therefore \angle BAC=\angle BCA$.
(2)$\because OA=OB$,$\therefore \angle ABO=\angle BAO=\frac{1}{2}(180^\circ -\angle AOB)$.同理,$\angle CBO=\angle BCO=\frac{1}{2}(180^\circ -\angle BOC)$.又$\because \angle AOB=\angle BOC$,$\therefore \angle ABO=\angle CBO$.
(1)$\because \angle AOB=\angle BOC$,$\therefore \overset{\frown}{AB}=\overset{\frown}{BC}$,$BA=BC$,$\therefore \angle BAC=\angle BCA$.
(2)$\because OA=OB$,$\therefore \angle ABO=\angle BAO=\frac{1}{2}(180^\circ -\angle AOB)$.同理,$\angle CBO=\angle BCO=\frac{1}{2}(180^\circ -\angle BOC)$.又$\because \angle AOB=\angle BOC$,$\therefore \angle ABO=\angle CBO$.
查看更多完整答案,请扫码查看


