第39页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
9. 如图,AB,BC,CD是某正多边形相邻的三条边,延长AB,DC交于点P,若∠P= 108°,则该正多边形的边数为
]
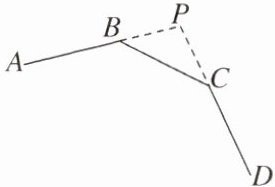
10
.]

答案:
10
10. 作图与证明:如图,已知⊙O和⊙O上的一点A,请完成下列任务:
(1)作⊙O的内接正六边形ABCDEF.
(2)连结BF,CE,判断四边形BCEF的形状并加以证明.
]
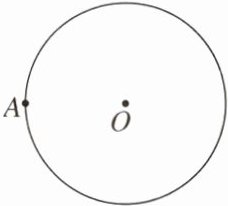
(1)作⊙O的内接正六边形ABCDEF.
(2)连结BF,CE,判断四边形BCEF的形状并加以证明.
]

答案:
解:
(1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交⊙O于点B,F,C,E,连结AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求作的图形.


(2)四边形BCEF是矩形.
证明:如图2,连结OE.
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC=FE=BC,
∴$\overset{\frown}{AB}=\overset{\frown}{AF}=\overset{\frown}{DE}=\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}=\overset{\frown}{CE}$,
∴BF=CE,
∴四边形BCEF是平行四边形.
∵∠EOD=60°,OE=OD,
∴△EOD是等边三角形,
∴∠OED=∠ODE=60°,
∴∠EDC=∠FED=2∠ODE=120°.
∵DE=DC,
∴∠DEC=∠DCE=30°,
∴∠CEF=∠DEF−∠CED=90°,
∴四边形BCEF是矩形.
解:
(1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交⊙O于点B,F,C,E,连结AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求作的图形.


(2)四边形BCEF是矩形.
证明:如图2,连结OE.
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC=FE=BC,
∴$\overset{\frown}{AB}=\overset{\frown}{AF}=\overset{\frown}{DE}=\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}=\overset{\frown}{CE}$,
∴BF=CE,
∴四边形BCEF是平行四边形.
∵∠EOD=60°,OE=OD,
∴△EOD是等边三角形,
∴∠OED=∠ODE=60°,
∴∠EDC=∠FED=2∠ODE=120°.
∵DE=DC,
∴∠DEC=∠DCE=30°,
∴∠CEF=∠DEF−∠CED=90°,
∴四边形BCEF是矩形.
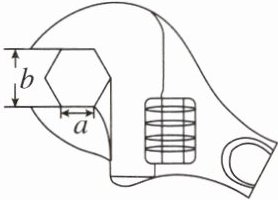
11. 如图,要拧开一个边长a= 8 mm的正六边形螺帽,扳手张开的开口b至少为(
A.$8\sqrt{2}\ mm$
B.$16\ mm$
C.$8\sqrt{3}\ mm$
D.$4\ mm$
C
)
A.$8\sqrt{2}\ mm$
B.$16\ mm$
C.$8\sqrt{3}\ mm$
D.$4\ mm$
答案:
C
12. 阅读图中的材料,解答问题:已知⊙O是一个正十二边形的外接圆,该外接圆的半径为1,如果用这个正十二边形的面积来近似估计⊙O的面积,则⊙O的面积约为

3
.
答案:
3
13. 如图,A,B,C,D,E是⊙O上的五等分点,连结AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)求∠CAD的度数.
(2)连结AE,求证:AE= ME.
]
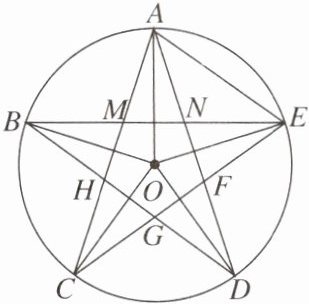
(1)求∠CAD的度数.
(2)连结AE,求证:AE= ME.
]

答案:
解:
(1)
∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD=$\frac{360^\circ}{5}$=72°,
∴∠CAD=$\frac{1}{2}$∠COD=36°.
(2)证明:同
(1)可得∠EBD=∠BDA=36°.
∵∠AEB=∠BDA,∠DAE=∠EBD,∠CAD=36°,
∴∠MAE=72°,∠AEB=36°,
∴∠AME=180°−72°−36°=72°,
∴∠MAE=∠AME,
∴AE=ME.
(1)
∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD=$\frac{360^\circ}{5}$=72°,
∴∠CAD=$\frac{1}{2}$∠COD=36°.
(2)证明:同
(1)可得∠EBD=∠BDA=36°.
∵∠AEB=∠BDA,∠DAE=∠EBD,∠CAD=36°,
∴∠MAE=72°,∠AEB=36°,
∴∠AME=180°−72°−36°=72°,
∴∠MAE=∠AME,
∴AE=ME.
查看更多完整答案,请扫码查看


