第41页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
9. 已知某扇形的圆心角为 $120^\circ$,面积为 $\frac{25}{3\pi} \, cm^2$,求该扇形的弧长.
答案:
解:设该扇形的半径为 R(cm).
∵扇形的圆心角为 120°,面积为$\frac{25}{3}$πcm²,
∴$\frac{120×π×R²}{360}$=$\frac{25}{3}$π,
∴πR = 5(负值舍去),
∴l = $\frac{120}{180}$πR = $\frac{2}{3}$×5 = $\frac{10}{3}$(cm).
∵扇形的圆心角为 120°,面积为$\frac{25}{3}$πcm²,
∴$\frac{120×π×R²}{360}$=$\frac{25}{3}$π,
∴πR = 5(负值舍去),
∴l = $\frac{120}{180}$πR = $\frac{2}{3}$×5 = $\frac{10}{3}$(cm).
10. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花. 图 1 中外侧的摆盘,其形状是扇形的一部分,图 2 是其几何示意图(阴影部分为摆盘),通过测量得到 $AC = BD = 12 \, cm$,C,D 两点之间的距离为 3 cm,圆心角为 $60°$,则图 2 中摆盘的面积是 (
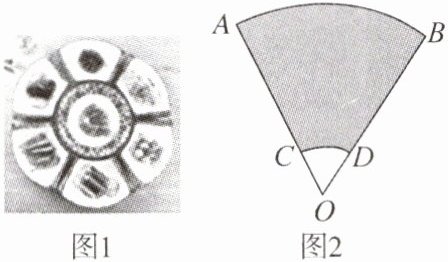
A.$12\pi \, cm^2$
B.$24\pi \, cm^2$
C.$36\pi \, cm^2$
D.$48\pi \, cm^2$
C
) 
A.$12\pi \, cm^2$
B.$24\pi \, cm^2$
C.$36\pi \, cm^2$
D.$48\pi \, cm^2$
答案:
C
11. 如图,在扇形 AOB 中,$\angle AOB = 120^\circ$,$OA = 5$,C 是 $\overset{\frown}{AB}$ 的中点,D 为半径 OA 上一点,则图中阴影部分的面积为 $______$.
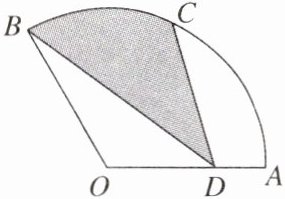

答案:
$\frac{25}{6}$π [解析]连结 OC,BC,
由题意得,∠AOC = ∠BOC = $\frac{1}{2}$∠AOB = 60°,
∵OB = OC,
∴△BOC 是正三角形,
∴∠OCB = ∠AOC = 60°,
∴BC//OA,
∴$S_{\triangle BCD}=S_{\triangle BCO}$,

∴$S_{阴影}=S_{扇形 BOC}=\frac{60π×5²}{360}=\frac{25}{6}$π.
$\frac{25}{6}$π [解析]连结 OC,BC,
由题意得,∠AOC = ∠BOC = $\frac{1}{2}$∠AOB = 60°,
∵OB = OC,
∴△BOC 是正三角形,
∴∠OCB = ∠AOC = 60°,
∴BC//OA,
∴$S_{\triangle BCD}=S_{\triangle BCO}$,

∴$S_{阴影}=S_{扇形 BOC}=\frac{60π×5²}{360}=\frac{25}{6}$π.
12. 如图,ABCD 是围墙,$AB // CD$,$\angle ABC = 120^\circ$,有一根 6 m 长的绳子,一端拴在围墙一角的柱子 B 处,另一端 E 处拴着一只羊,求这只羊活动区域的最大面积.


答案:
解:如图,扇形 FBG 和扇形 GCH 为羊活动的区域.$S_{扇形 FBG}=\frac{120π×6²}{360}=12π$(m²),
$S_{扇形 GCH}=\frac{60π×2²}{360}=\frac{2}{3}$π(m²),
∴这只羊活动区域的最大面积为$12π+\frac{2}{3}π=\frac{38}{3}π$(m²).

解:如图,扇形 FBG 和扇形 GCH 为羊活动的区域.$S_{扇形 FBG}=\frac{120π×6²}{360}=12π$(m²),
$S_{扇形 GCH}=\frac{60π×2²}{360}=\frac{2}{3}$π(m²),
∴这只羊活动区域的最大面积为$12π+\frac{2}{3}π=\frac{38}{3}π$(m²).

查看更多完整答案,请扫码查看


