第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 周长是4 m的矩形,它的面积$S(m^2)$与一边长x(m)之间的函数图象大致是 (
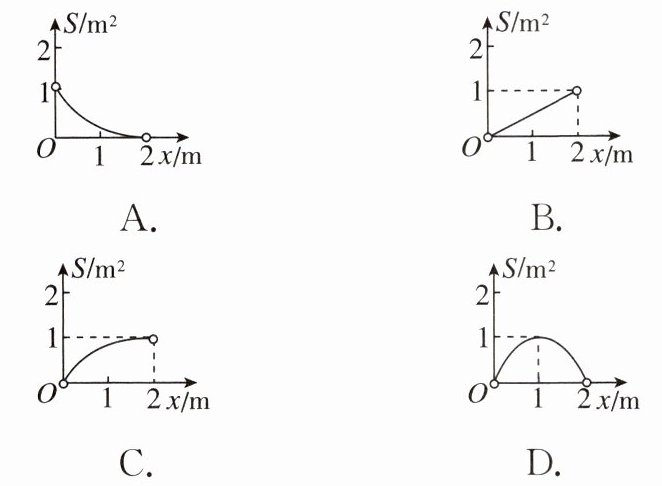
D
)
答案:
D
2. 如图,在△ABC中,∠C= 90°,AB= 10 cm,BC= 8 cm,点P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积的最小值为 (
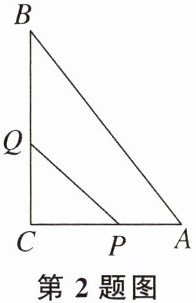
A.$19 cm^2$
B.$16 cm^2$
C.$12 cm^2$
D.$15 cm^2$
D
)
A.$19 cm^2$
B.$16 cm^2$
C.$12 cm^2$
D.$15 cm^2$
答案:
D
3. 在一块等腰直角三角形铁皮上截一块矩形铁皮.如图,已有的铁皮是等腰直角三角形ABC,它的底边AB长20厘米.要截得的矩形DEMN的边MN在AB上,顶点D,E分别在边AC,BC上,设DE的长为x厘米,矩形DEMN的面积为y平方厘米,那么y关于x的函数表达式是
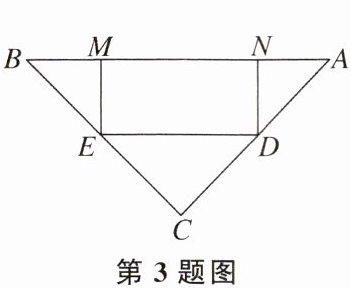
y = -$\frac{1}{2}$x² + 10x
.(不用写出x的取值范围)
答案:
y = -$\frac{1}{2}$x² + 10x
4. 如图,线段AB= 10,点P在线段AB上,在AB的同侧分别以AP,BP为边作正方形APCD和正方形BPEF,M,N分别是EF,CD的中点,则MN的最小值是
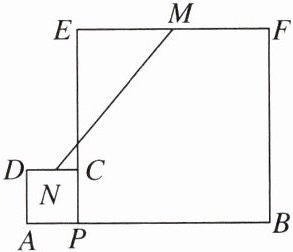
5
.
答案:
5
5. 如图,抛物线$y= -x^{2}+bx+c$经过A(-1,0),B(3,0)两点,D为抛物线的顶点,连结BD,H为BD的中点.
(1)求抛物线的函数表达式及顶点D的坐标.
(2)若在直线x= 1上存在一点P,使得PB+PH的值最小,求PB+PH的最小值.

(1)求抛物线的函数表达式及顶点D的坐标.
(2)若在直线x= 1上存在一点P,使得PB+PH的值最小,求PB+PH的最小值.

答案:
解:
(1)
∵抛物线y = - x² + bx + c过点A(- 1,0),B(3,0),
∴$\begin{cases} -1-b+c=0, \\ -9+3b+c=0 \end{cases}$解得$\begin{cases} b=2, \\ c=3 \end{cases}$,
∴抛物线的函数表达式为y = - x² + 2x + 3.
∵y = - x² + 2x + 3 = -(x - 1)² + 4,
∴顶点D的坐标为(1,4).
(2)
∵点B(3,0),D(1,4),
∴BD中点H的坐标为(2,2),其关于直线x = 1的对称点H'的坐标为(0,2).
连结H'B(图略),与直线x = 1相交于点P,则此时PB + PH的值最小,最小值为$\sqrt{3^2 + 2^2}$ = $\sqrt{13}$.
(1)
∵抛物线y = - x² + bx + c过点A(- 1,0),B(3,0),
∴$\begin{cases} -1-b+c=0, \\ -9+3b+c=0 \end{cases}$解得$\begin{cases} b=2, \\ c=3 \end{cases}$,
∴抛物线的函数表达式为y = - x² + 2x + 3.
∵y = - x² + 2x + 3 = -(x - 1)² + 4,
∴顶点D的坐标为(1,4).
(2)
∵点B(3,0),D(1,4),
∴BD中点H的坐标为(2,2),其关于直线x = 1的对称点H'的坐标为(0,2).
连结H'B(图略),与直线x = 1相交于点P,则此时PB + PH的值最小,最小值为$\sqrt{3^2 + 2^2}$ = $\sqrt{13}$.
查看更多完整答案,请扫码查看


