《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

9. 如图,在平面直角坐标系中,$\triangle ABC的三个顶点坐标分别为A(0,3)$,$B(-1,0)$,$C(3,-1)$(每个方格的边长均为1个单位长度).
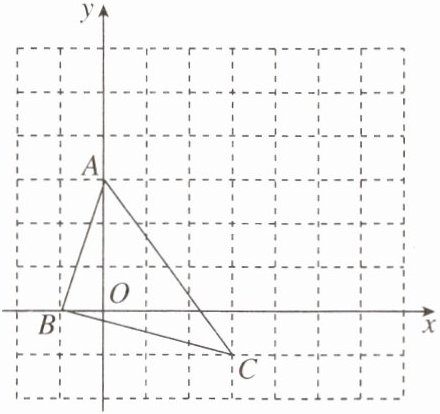
(1)将$\triangle ABC绕点A逆时针旋转90^\circ$,画出旋转后得到的$\triangle AB_1C_1$.
(2)直接写出在旋转过程中,点$C$经过的格点坐标($C$,$C_1$除外,格点指小正方形的顶点).

答案：
解:
(1)如图,△AB₁C₁即为所求.
　　　　　　
(2)点C经过的格点坐标为(4,0),(5,3).

10. 如图,在正方形网格中,$\triangle EFG绕某一点旋转某一角度得到\triangle RPQ$.则旋转中心可能是(C)

A.点$A$
B.点$B$
C.点$C$
D.点$D$

答案： C

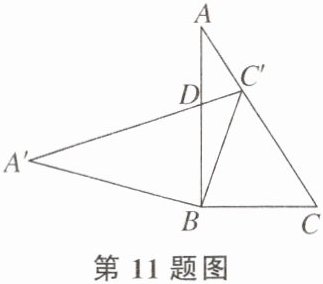
11. 如图,在$\triangle ABC$中,$\angle ABC= 90°$,$\angle C= 55°$,将$\triangle ABC绕点B逆时针旋转得到\triangle A'BC'$,若点$C'恰好落在线段AC$上,$AB$,$A'C'相交于点D$,则$\angle A'DB$的度数是75°.

答案： 75°

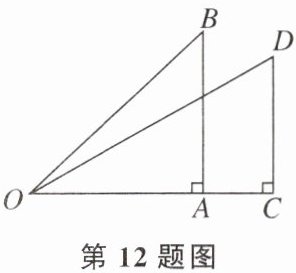
12. 如图,将一副三角板重叠放置,其中$30°和45°$的两个角的顶点重合在一起.若将三角板$AOB绕点O$旋转,在旋转过程中,当$AB// OC$时,$\angle BOC= $45°或135°.

答案： 45°或135°

13. 如图,线段$MN= 4$,点$A在线段MN$上,且$AM= 1$,$B为线段AN$上的一个动点.以$A为中心顺时针旋转点M$,以$B为中心逆时针旋转点N$,旋转角分别为$\alpha和\beta$.若旋转后$M$,$N两点重合成一点C$(即构成$\triangle ABC$),设$AB= x$.
(1)$\triangle ABC$的周长为4.
(2)若$\alpha+\beta=270°$,求$x$的值.

答案： 解:
(1)由旋转知,AM=AC=1,BN=BC=3-x,
∵△ABC的周长为AC+AB+BC=MN=4,故答案为4.
(2)
∵α+β=270°,
∴∠CAB+∠CBA=360°-270°=90°,
∴∠ACB=180°-(∠CAB+∠CBA)=180°-90°=90°,
∴AC²+BC²=AB²,
　　即1²+(3-x)²=x²,
　　解得x=$\frac{5}{3}$.