《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

10. 已知一次函数 $y= kx+b(k≠0)$,若 k 从 2,-3 中随机取一个值,b 从 1,-1,-2 中随机取一个值,则该一次函数的图象经过第二、三、四象限的概率是(A)
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{5}{6}$

答案： A

11. 某地区人口状况相对稳定,某保险公司根据多年统计综合,有一张关于该地区人口寿命的表格,现摘录部分内容如下.

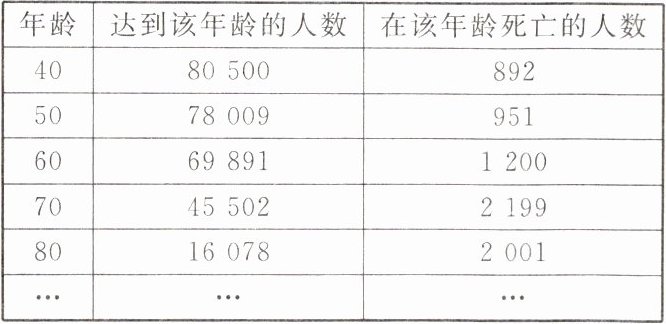
则该地区达到 50 岁的人中,不能达到 51 岁的概率约为0.012,能达到 80 岁的概率约为0.206.(结果精确到 0.001)

答案： 0.012　0.206

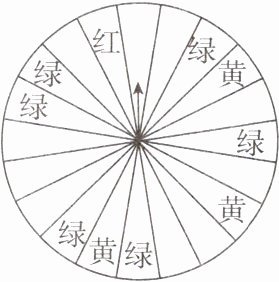
12. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被平均分为 20 份),并规定：顾客每购买 200 元的商品,就能获得一次转动转盘的机会. 如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得 200 元、100 元、50 元的购物券,凭购物券可以在该商场继续购物. 如果顾客不愿意转转盘,那么可以直接获得购物券 30 元.
(1)求转动一次转盘获得购物券的概率.
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算？

答案： 解:
(1)
∵转盘被平均分为20份,转动一次转盘获得购物券的情况有10种，
∴P(转动一次转盘获得购物券)=$\frac{10}{20}$=$\frac{1}{2}$.
(2)
∵P(红色)=$\frac{1}{20}$、P(黄色)=$\frac{3}{20}$,P(绿色)=$\frac{6}{20}=\frac{3}{10}$,
∴200×$\frac{1}{20}$+100×$\frac{3}{20}$+50×$\frac{3}{10}$=40(元).
∵40元＞30元，
∴选择转转盘对顾客更合算.