第56页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
【例1】为了测量河宽AB,某同学采用以下方法:如图,取一根标尺CD,使CD//AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD= 10米,OC= 15米,OA= 45米,则河宽AB=
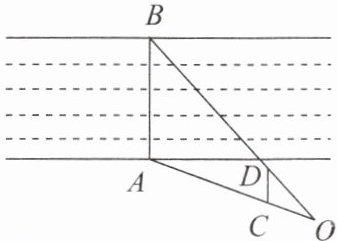
30
米.
答案:
30
【变式】如图,△ADE∽△ACB,BC= 5,$S_{\triangle ADE}:S_{四边形BCED}= 9:16$,则DE=
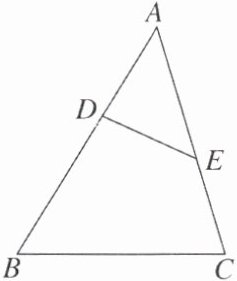
3
.
答案:
3
【例2】如图,AB//CD,AD与BC相交于点O,AB:CD= 1:2,OB= 2,那么BC= (

A.4
B.5
C.6
D.8
C
)
A.4
B.5
C.6
D.8
答案:
C
【变式】如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,AF与DE相交于点G,则$\frac{AG}{FG}$的值是( )
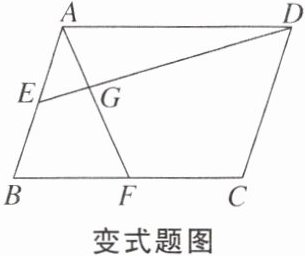
A.$\frac{2}{3}$
B.$\frac{3}{2}$
C.$\frac{3}{4}$
D.$\frac{3}{5}$

A.$\frac{2}{3}$
B.$\frac{3}{2}$
C.$\frac{3}{4}$
D.$\frac{3}{5}$
答案:
A [解析]如图所示,延长DE,CB相交于点H.
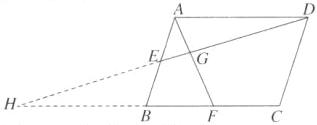
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴∠ADE=∠H,且AE=BE,∠AED=∠BEH,
∴△ADE≌△BHE(AAS),
∴BH=AD.
∵F是BC的中点,
∴BF=$\frac{1}{2}$BC,
∴HF=BH+BF=$\frac{3}{2}$BC=$\frac{3}{2}$AD.
∵AD//HF,
∴△ADG∽△FHG,
∴$\frac{AG}{FG}$=$\frac{AD}{HF}$=$\frac{AD}{\frac{3}{2}AD}$ = $\frac{2}{3}$.
A [解析]如图所示,延长DE,CB相交于点H.

∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴∠ADE=∠H,且AE=BE,∠AED=∠BEH,
∴△ADE≌△BHE(AAS),
∴BH=AD.
∵F是BC的中点,
∴BF=$\frac{1}{2}$BC,
∴HF=BH+BF=$\frac{3}{2}$BC=$\frac{3}{2}$AD.
∵AD//HF,
∴△ADG∽△FHG,
∴$\frac{AG}{FG}$=$\frac{AD}{HF}$=$\frac{AD}{\frac{3}{2}AD}$ = $\frac{2}{3}$.
【例3】如图,在Rt△ABC中,∠ACB= 90°,CD是斜边AB上的高,AC= 3,BC= 4.
(1)求CD和AD的长.
(2)求证:AC是AD和AB的比例中项.
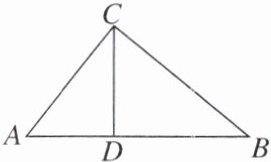
(1)求CD和AD的长.
(2)求证:AC是AD和AB的比例中项.

答案:
(1)
∵∠ACB=90°,AC=3,BC=4,
∴AB= $\sqrt{AC^2+BC^2}$ =5.
∵$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC= $\frac{1}{2}$AB·CD,
∴CD= $\frac{AC·BC}{AB}$ = $\frac{12}{5}$.
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴AD= $\sqrt{AC^2-CD^2}$ = $\frac{9}{5}$.
(2)证明:
∵∠ADC=∠ACB=90°,∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AD}{AC}$ = $\frac{AC}{AB}$,
∴AC²=AD·AB,
∴AC是AD和AB的比例中项.
(1)
∵∠ACB=90°,AC=3,BC=4,
∴AB= $\sqrt{AC^2+BC^2}$ =5.
∵$S_{\triangle ABC}$ = $\frac{1}{2}$AC·BC= $\frac{1}{2}$AB·CD,
∴CD= $\frac{AC·BC}{AB}$ = $\frac{12}{5}$.
∵CD是斜边AB上的高,
∴∠ADC=90°,
∴AD= $\sqrt{AC^2-CD^2}$ = $\frac{9}{5}$.
(2)证明:
∵∠ADC=∠ACB=90°,∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AD}{AC}$ = $\frac{AC}{AB}$,
∴AC²=AD·AB,
∴AC是AD和AB的比例中项.
【变式】如图,△ACP∽△ABC,若∠A= 100°,∠ACP= 20°,则∠PCB的度数是(
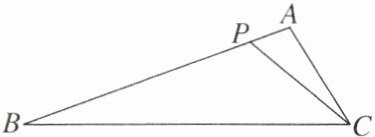
A.60°
B.50°
C.40°
D.30°
C
)
A.60°
B.50°
C.40°
D.30°
答案:
C
【例4】如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF= 3,则小正方形的边长为(
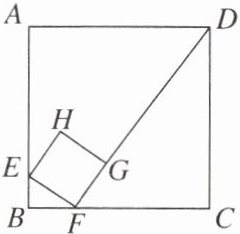
A.$\frac{15}{4}$
B.$2\sqrt{3}$
C.5
D.6
A
)
A.$\frac{15}{4}$
B.$2\sqrt{3}$
C.5
D.6
答案:
A
查看更多完整答案,请扫码查看


