《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

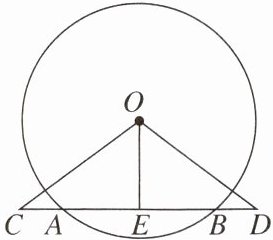
9. 如图,AB 是$\odot O$的弦,C,D 是直线 AB 上的两点,并且$AC= BD$,OE 是$\triangle OCD$的中线.求证:$\angle C= \angle D$.

答案： 证明：
∵OE 是△OCD 的中线，
∴CE=DE.
∵AC=BD，
∴AE=BE，
∴OE⊥AB.
又
∵CE=DE，
∴在△OCD 中，直线 OE 是 CD 的中垂线，
∴OC=OD，
∴∠C=∠D.

10. 某校科技实践社团制作实践设备,小明的操作过程如下：

①小明取出老师提供的圆形细铁环,先通过在圆这一章中学到的知识找到圆心 O,再任意找出圆 O 的一条直径标记为 AB(如图 1),测量出$AB= 4$分米.
②将圆环进行翻折,使点 B 落在圆心 O 的位置,翻折部分的圆环和未翻折的圆环产生的交点分别标记为 C,D(如图 2).
③用一细橡胶棒连结 C,D 两点(如图 3),计算出橡胶棒 CD 的长度.
那么橡胶棒 CD 的长度为(B)
A.$2\sqrt{2}$分米
B.$2\sqrt{3}$分米
C.$3\sqrt{2}$分米
D.$3\sqrt{3}$分米

答案： B

11. 某地有很多历史悠久的石拱桥,它们是圆弧的桥梁.如图,这是某石拱桥的局部,其跨度 AB 为 24 米,拱高 CD 为 4 米,则这个弧形石拱桥设计的半径为20米.

答案： 20

12. 如图,$\odot O$经过矩形 ABCD 的顶点 C,且与 AD 相交于点 E,F,与 BC 相交于点 H,AD,BC 在圆心 O 的同侧.已知$AE= EF= 4$,$BH= 3$.

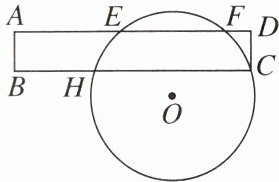
(1)CH 的长为6.
(2)若$\odot O的半径为\sqrt{10}$,则$AB= $$\sqrt{6}-1$.

答案：

(1)6

(2)$\sqrt{6}-1$

13. 如图,这是正在修建的某大门上半部分的截面,其为圆弧形,跨度 CD(弧所对的弦)的长为 3.2 米,拱高 AB(弧的中点到弦的距离)为 0.8 米.

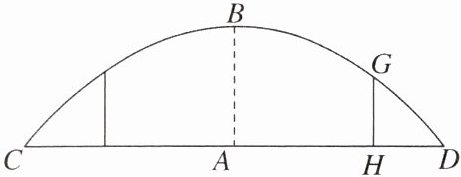
(1)求该圆弧所在圆的半径.
(2)在修建中,在距大门边框的一端(点 D)0.4 米处将竖立支撑杆 HG,求支撑杆 HG 的高度.

答案： 解：
(1)
∵AB 垂直平分 CD，
∴圆心 O 在 BA 的延长线上，
连结 OC，如图，设⊙O 的半径为 r(米)，则 OA=(r-0.8)米，
∵OB⊥CD，
∴CA=DA=$\frac{1}{2}$CD=$\frac{1}{2}×3.2=1.6$(米).
在 Rt△OAC 中，$1.6^{2}+(r-0.8)^{2}=r^{2}$，
解得 r=2，即该圆弧所在圆的半径为 2 米.
(2)过点 G 作 GE⊥AB 于点 E，连结 OG，如图，
∵DH=0.4 米，
∴AH=AD-DH=1.2 米.
∵∠GEA=∠EAH=∠GHA=90°，
∴四边形 AHGE 为矩形，
∴AE=GH，GE=AH=1.2 米.
在 Rt△OEG 中，OE=$\sqrt{OG^{2}-EG^{2}}=\sqrt{2^{2}-1.2^{2}}$=1.6(米)，
∵OA=OB-AB=2-0.8=1.2(米)，
∴AE=OE-OA=1.6-1.2=0.4(米)，
∴GH=0.4 米，
即支撑杆 HG 的高度为 0.4 米.