《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

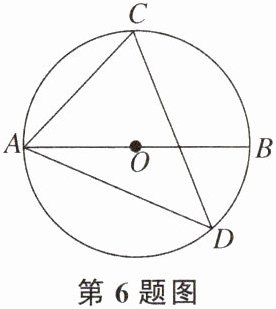
6. 如图,AB是⊙O的直径,CD是⊙O的弦,连结AC,AD,若∠ACD＝65°,则∠BAD的度数为25°.

答案： 25°

7. 如图,A,B,C,D,E都是⊙O上的点,AC＝AE,∠D＝128°,则∠B＝______°.

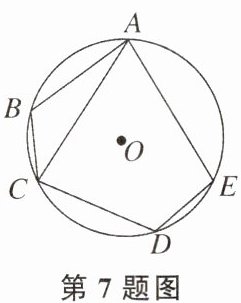
答案：
116　[解析]连结CE,如图.
∵A,C,D,E都是⊙O上的点,
∴∠CAE+∠D=180°,
　　　　　　　　　　　　　　　　　
∴∠CAE=180°-128°=52°.
∵AC=AE,
∴∠ACE=∠AEC=$\frac{1}{2}$×(180°-52°)=64°.
∵A,B,C,E都是⊙O上的点,
∴∠AEC+∠B=180°,
∴∠B=180°-64°=116°.

8. 如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与弧AB交于点C,连结AC.若OA＝3,则图中阴影部分的面积是______.(结果保留π)

答案：
$\frac{3\pi}{2}-\frac{9\sqrt{3}}{4}$　[解析]连结OC,如图,
　　由折叠可知,AC=OC.
∵OC=OA,
∴AC=OC=OA,
∴△ACO是等边三角形，
∴∠AOC=60°,OC=3,
　　　　　　　　　　　　　　　
∴S_扇形AOC=$\frac{60° × \pi × 3^2}{360°}$=$\frac{3}{2}\pi$.
∵CD=CO·sin∠AOC=$\frac{3\sqrt{3}}{2}$,
∴S_△AOC=$\frac{1}{2} × CD × AO$=$\frac{9\sqrt{3}}{4}$,
∵阴影部分的面积=S_扇形AOC-S_△AOC,
∴阴影部分的面积=$\frac{3}{2}\pi-\frac{9\sqrt{3}}{4}$.

9. (1)请借助网格和一把无刻度直尺找出△ABC的外心点O.
(2)设每个小方格的边长为1,求出外接圆⊙O的面积.

答案：
解:
(1)如图所示,点O即为所求.
　　　　　　　　　
(2)连结OB,
　　由勾股定理得OB= $\sqrt{3^2 + 1^2}$=$\sqrt{10}$,
∴外接圆⊙O的面积为π×($\sqrt{10}$)²=10π.

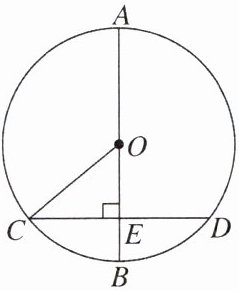
10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE＝3,CD＝8.
(1)求CE的长度.
(2)求OC的长度.

答案： 解:
(1)
∵直径AB⊥CD,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4.
(2)
∵∠OEC=90°,OE=3,CE=4,
∴OC= $\sqrt{OE^2 + CE^2}$=5.

11. 如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证：CF＝BF.
(2)若AD＝6,⊙O的半径为5,求BC的长.

答案：
解:
(1)证明:连结AC,如图1所示.
∵C是$\stackrel{\frown }{BD}$的中点,
∴∠DBC=∠BAC.
　　在△ABC中,∠ACB=90°.
　　又
∵CE⊥AB,
∴∠AEC=90°,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
∴∠BCE=∠DBC,
∴CF=BF.
　　　　　　
(2)连结OC交BD于点G,如图2所示
∵AB是⊙O的直径,
∴AB=2OC=10,∠ADB=90°,
∴BD= $\sqrt{AB^2 - AD^2}$=$\sqrt{10^2 - 6^2}$=8.
∵C是$\stackrel{\frown }{BD}$的中点,
∴OC⊥BD,DG=BG=$\frac{1}{2}$BD=4.
∵OA=OB,
∴OG是△ABD的中位线,
∴OG=$\frac{1}{2}$AD=3,
∴CG=OC-OG=5-3=2.
　　在Rt△BCG中,由勾股定理得，BC=$\sqrt{CG^2 + BG^2}$=$\sqrt{2^2 + 4^2}$=2$\sqrt{5}$.