第62页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 如图,$\odot O是\triangle ABC$的外接圆,$\angle BAC$的平分线与 BC 边和外接圆分别相交于点 D 和 E,则图中相似三角形共有 (
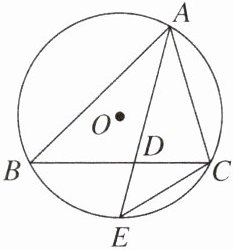
A.1 对
B.2 对
C.3 对
D.4 对
C
)
A.1 对
B.2 对
C.3 对
D.4 对
答案:
C
2. 下图是小明实验小组成员在小孔成像实验中的影像,蜡烛在刻度尺 50 cm 处,遮光板在刻度尺 70 cm 处,光屏在刻度尺 80 cm 处,量得像高 3 cm,则蜡烛的长为 (
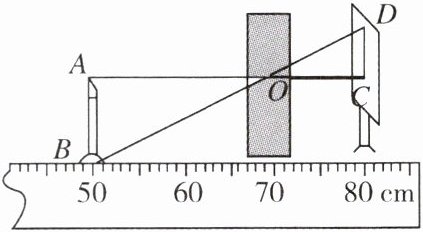
A.5 cm
B.6 cm
C.4 cm
D.4.5 cm
B
)
A.5 cm
B.6 cm
C.4 cm
D.4.5 cm
答案:
B
3. 如图,AB 是半圆 O 的直径,C 是半圆 O 上一点,弦 AD 平分$\angle BAC$,交 BC 于点 E.若 AB= 6,AD= 5,则 DE 的长为 ( )
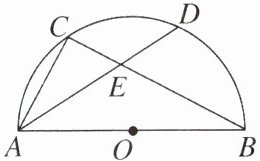
A.$\frac{11}{5}$
B.$\frac{14}{5}$
C.1
D.$\frac{5}{3}$

A.$\frac{11}{5}$
B.$\frac{14}{5}$
C.1
D.$\frac{5}{3}$
答案:
3. A 【解析】如图,连结 BD,CD,
∵AB 为半圆 O 的直径,
∴∠ADB=90°,
∴BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{6^{2}-5^{2}}=\sqrt{11}$.
∵弦 AD 平分∠BAC,
∴CD=BD=$\sqrt{11}$,
∴∠CBD=∠DAB.
∵∠BAD=∠EBD,∠ADB=∠BDE,
∴△ABD∽△BED,
∴$\frac{DE}{DB}=\frac{DB}{AD}$,
∴$\frac{DE}{\sqrt{11}}=\frac{\sqrt{11}}{5}$,
解得 DE=$\frac{11}{5}$.

3. A 【解析】如图,连结 BD,CD,
∵AB 为半圆 O 的直径,
∴∠ADB=90°,
∴BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{6^{2}-5^{2}}=\sqrt{11}$.
∵弦 AD 平分∠BAC,
∴CD=BD=$\sqrt{11}$,
∴∠CBD=∠DAB.
∵∠BAD=∠EBD,∠ADB=∠BDE,
∴△ABD∽△BED,
∴$\frac{DE}{DB}=\frac{DB}{AD}$,
∴$\frac{DE}{\sqrt{11}}=\frac{\sqrt{11}}{5}$,
解得 DE=$\frac{11}{5}$.

4. 如图,某校宣传栏 BC 后面 12 米处种有一排与宣传栏平行的若干棵树,即 BC$//$ED,且相邻两棵树的间隔为 2 米,一人站在距宣传栏前面的 A 处正好看到两端的树干,其余的树均被宣传栏挡住.已知 AF$\perp$BC,AF= 3 米,BC= 10 米,则该宣传栏后 DE 处共有

26
棵树.(不计宣传栏的厚度).
答案:
26
5. 如图,在矩形 ABCD 中,BC= 8,AB= 6,E 为 BC 边上一个动点(不与点 B,C 重合),连结 AE,过点 E 作 EF$\perp$AE 交 CD 于点 F,则 CF 的最大值是
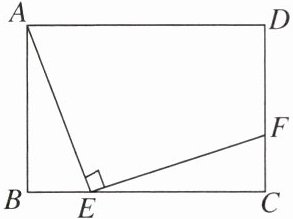
$\frac{8}{3}$
.
答案:
$\frac{8}{3}$
6. 如图,一条 4 m 宽的道路将矩形花坛分成一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为
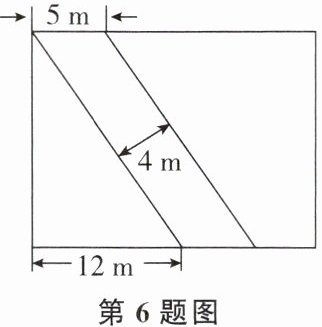
80 m²
.
答案:
80 m²
7. 如图,已知 AB 是圆 O 的直径,$\angle DPB= 60^\circ$,则 CD∶AB= ______.
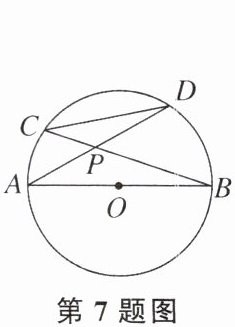

答案:
7. 1:2 【解析】连结 BD,如图.
∵AB 是圆 O 的直径,
∴∠ADB=90°.
∵∠DPB=60°,
∴∠DBP=180° - 90° - 60°=30°,
∴BP=2PD.
∵∠C=∠A,∠CDP=∠ABP,
∴△CPD∽△APB,
∴$\frac{CD}{AB}=\frac{DP}{BP}=\frac{DP}{2DP}=\frac{1}{2}$,
即 CD:AB=1:2.

7. 1:2 【解析】连结 BD,如图.
∵AB 是圆 O 的直径,
∴∠ADB=90°.
∵∠DPB=60°,
∴∠DBP=180° - 90° - 60°=30°,
∴BP=2PD.
∵∠C=∠A,∠CDP=∠ABP,
∴△CPD∽△APB,
∴$\frac{CD}{AB}=\frac{DP}{BP}=\frac{DP}{2DP}=\frac{1}{2}$,
即 CD:AB=1:2.

查看更多完整答案,请扫码查看


