第60页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
【例 3】操场上有一根竖直的旗杆 AB,它的一部分影子(BC)落在水平地面上,另一部分影子(CD)落在对面的墙壁上,经测量,墙壁上的影高为 1.2 m,地面上的影长为 2.8 m,同时测得一根高为 2 m 的竹竿 OM 的影长是 ON= 1.4 m,则根据以上信息,可以求得旗杆的高度是(
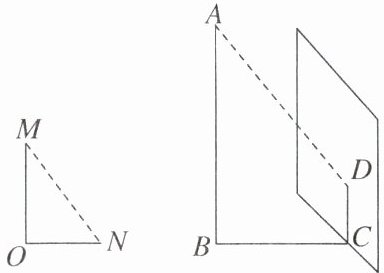
A.4.5 m
B.104.7 m
C.5.2 m
D.5.7 m
C
)
A.4.5 m
B.104.7 m
C.5.2 m
D.5.7 m
答案:
C
【变式】“计里画方”(比例缩放和直角坐标网格体系)是中国古代地图制图的基本方法和数学基础,是中国古代地图独立发展的重要标志.制作地图时,人们会利用测杆、水准仪和照板来测量距离.如图,在测量距离 AB 的示意图中,记照板“内芯”的高度为 EF.观测者的眼睛(图中用点 C 表示)与 BF 在同一水平线上,若某次测量中$\frac{CF}{BF}= \frac{1}{5}$,则下列结论中错误的是 (
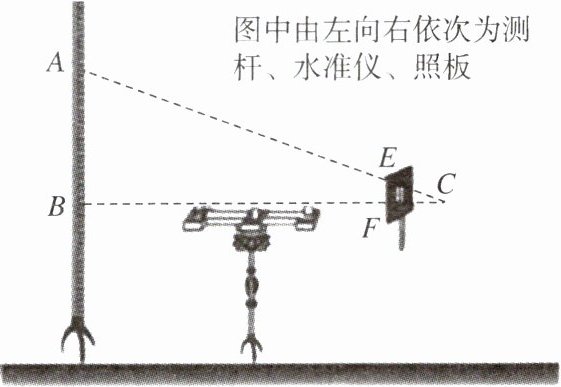
A.$\frac{CE}{AE}= \frac{1}{5}$
B.$\frac{EF}{AB}= \frac{1}{6}$
C.$\frac{CF}{CE}= \frac{1}{2}$
D.$\frac{S_{\triangle CEF}}{S_{\triangle CAB}}= \frac{1}{36}$
C
)
A.$\frac{CE}{AE}= \frac{1}{5}$
B.$\frac{EF}{AB}= \frac{1}{6}$
C.$\frac{CF}{CE}= \frac{1}{2}$
D.$\frac{S_{\triangle CEF}}{S_{\triangle CAB}}= \frac{1}{36}$
答案:
C
【例 4】如图,四边形 ABCD 内接于半圆 O,AB 是直径,C 是$\widehat{BD}$的中点,延长 AD,BC 交于点 E.
(1)求证:CE= CD.
(2)若 AB= 5,BC= $\sqrt{5}$,求 AD 的长.
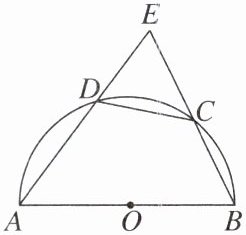
(1)求证:CE= CD.
(2)若 AB= 5,BC= $\sqrt{5}$,求 AD 的长.

答案:
解:
(1)证明:连结 AC,如图 1.
∵C 是 BD 的中点,
∴$\overset{\frown}{CD}=\overset{\frown}{CB}$,
∴∠EAC=∠BAC,CD=CB.
∵AB 是直径,
∴∠ACE=∠ACB=90°.
在△ACE 与△ACB 中,
$\left\{\begin{array}{l} ∠EAC=∠BAC,\\ AC=AC,\\ ∠ACE=∠ACB,\end{array}\right. $
∴△ACE≌△ACB(ASA),
∴BC=EC,
∴CD=CE.
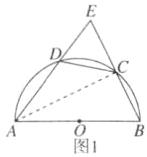
(2)连结 BD,如图 2.
由
(1)知,CE=BC=$\sqrt{5}$,
∴BE=BC+CE=$2\sqrt{5}$.
∵四边形 ABCD 内接于半圆 O,
∴∠ABC+∠ADC=180°.
∵∠ADC+∠CDE=180°,
∴∠ABC=∠CDE.
∵CE=CD,
∴∠E=∠CDE=∠ABC.
∵AB 为半圆 O 的直径,
∴∠ADB=90°,
∴∠BDE=90°.
∵∠ACB=∠BDE=90°,∠ABC=∠E,
∴△ABC∽△BED.
∴$\frac{AB}{BE}=\frac{BC}{ED}$,
∴$\frac{5}{2\sqrt{5}}=\frac{\sqrt{5}}{ED}$,
∴ED=2.
∵△ACE≌△ACB,
∴AE=AB=5,
∴AD=AE - ED=5 - 2=3.

解:
(1)证明:连结 AC,如图 1.
∵C 是 BD 的中点,
∴$\overset{\frown}{CD}=\overset{\frown}{CB}$,
∴∠EAC=∠BAC,CD=CB.
∵AB 是直径,
∴∠ACE=∠ACB=90°.
在△ACE 与△ACB 中,
$\left\{\begin{array}{l} ∠EAC=∠BAC,\\ AC=AC,\\ ∠ACE=∠ACB,\end{array}\right. $
∴△ACE≌△ACB(ASA),
∴BC=EC,
∴CD=CE.

(2)连结 BD,如图 2.
由
(1)知,CE=BC=$\sqrt{5}$,
∴BE=BC+CE=$2\sqrt{5}$.
∵四边形 ABCD 内接于半圆 O,
∴∠ABC+∠ADC=180°.
∵∠ADC+∠CDE=180°,
∴∠ABC=∠CDE.
∵CE=CD,
∴∠E=∠CDE=∠ABC.
∵AB 为半圆 O 的直径,
∴∠ADB=90°,
∴∠BDE=90°.
∵∠ACB=∠BDE=90°,∠ABC=∠E,
∴△ABC∽△BED.
∴$\frac{AB}{BE}=\frac{BC}{ED}$,
∴$\frac{5}{2\sqrt{5}}=\frac{\sqrt{5}}{ED}$,
∴ED=2.
∵△ACE≌△ACB,
∴AE=AB=5,
∴AD=AE - ED=5 - 2=3.

【变式】如图,AD 是$\odot O$的直径,以 A 为圆心,弦 AB 为半径画弧交$\odot O$于点 C,连结 BC 交 AD 于点 E,若 DE= 3,BC= 8,则$\odot O$的半径长为 ( )
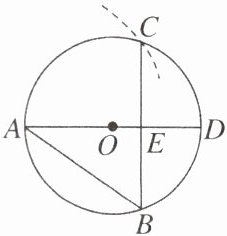
A.$\frac{25}{6}$
B.5
C.$\frac{16}{3}$
D.$\frac{25}{3}$

A.$\frac{25}{6}$
B.5
C.$\frac{16}{3}$
D.$\frac{25}{3}$
答案:
变式 A 【解析】连结 AC.
由题意,易得 AC=AB,
∴$\overset{\frown}{AB}=\overset{\frown}{AC}$,
∠ADB=∠ABE.
∵AD 为直径,
∴AD⊥BC,
∴BE=CE=$\frac{1}{2}$BC=4,∠BEA=∠BED=90°.
而∠BDE=∠ABE.
∴Rt△ABE∽Rt△BDE,
∴BE:DE=AE:BE,即 4:3=AE:4,
∴AE=$\frac{16}{3}$.
∴AD=AE+DE=$\frac{16}{3}+3=\frac{25}{3}$,
∴⊙O 的半径长为$\frac{25}{6}$.

变式 A 【解析】连结 AC.
由题意,易得 AC=AB,
∴$\overset{\frown}{AB}=\overset{\frown}{AC}$,
∠ADB=∠ABE.
∵AD 为直径,
∴AD⊥BC,
∴BE=CE=$\frac{1}{2}$BC=4,∠BEA=∠BED=90°.
而∠BDE=∠ABE.
∴Rt△ABE∽Rt△BDE,
∴BE:DE=AE:BE,即 4:3=AE:4,
∴AE=$\frac{16}{3}$.
∴AD=AE+DE=$\frac{16}{3}+3=\frac{25}{3}$,
∴⊙O 的半径长为$\frac{25}{6}$.

查看更多完整答案,请扫码查看


