《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

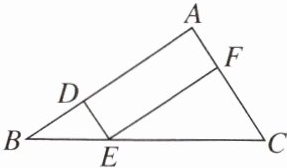
9. 如图,在△ABC 中,点 D,E,F 分别在 AB,BC,AC 边上,DE//AC,EF//AB.
(1)求证：△BDE∽△EFC.
(2)若$\frac{AF}{FC}= \frac{1}{2}$,△EFC 的面积是 20,求△ABC 的面积.

答案： 解:
(1)证明:
∵DE//AC,
∴∠DEB=∠FCE.
∵EF//AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC.
(2)
∵$\frac{AF}{FC}=\frac{1}{2}$,
∴$\frac{FC}{AC}=\frac{2}{3}$.
∵EF//AB,
∴△EFC∽△BAC,
∴$\frac{S_{\triangle EFC}}{S_{\triangle BAC}}=(\frac{FC}{AC})^2=(\frac{2}{3})^2=\frac{4}{9}$,
∴$S_{\triangle ABC}=\frac{9}{4}S_{\triangle EFC}=\frac{9}{4}×20=45$.

10. 如图,图 1 是装了液体的高脚杯,加入一些液体后如图 2 所示,则此时液面 AB 为 (B)

A.5.6 cm
B.6.4 cm
C.8 cm
D.10 cm

答案： B

11. 如图,D,E 分别是△ABC 的边 AB,BC 上的点,且 DE//AC,AE,CD 相交于点 O,若$S_{\triangle DOE}:S_{\triangle COA}= 1:9$,则$S_{\triangle BDE}:S_{\triangle CDE}= $1∶2.

答案： 1∶2

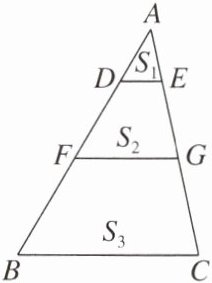
12. 如图,在△ABC 中,DE//FG//BC,并将△ABC 分成面积分别为$S_1$,$S_2$,$S_3$的三块.若$S_1:S_2:S_3= 1:4:10$,BC= 15,求 DE,FG 的长.

答案： 解:
∵DE//FG//BC,
∴△ADE∽△AFG∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^2$,$\frac{S_{\triangle AFG}}{S_{\triangle ABC}}=(\frac{FG}{BC})^2$,即$\frac{S_1}{S_1+S_2+S_3}=(\frac{DE}{15})^2$,$\frac{S_1+S_2}{S_1+S_2+S_3}=(\frac{FG}{15})^2$.设$S_1=k$,则$S_2=4k$,$S_3=10k$,
∴$\frac{S_1}{S_1+S_2+S_3}=\frac{k}{k+4k+10k}=(\frac{DE}{15})^2$,$\frac{S_1+S_2}{S_1+S_2+S_3}=\frac{k+4k}{k+4k+10k}=(\frac{FG}{15})^2$,
∴$DE=\sqrt{15}$,$FG=5\sqrt{3}$.