第14页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
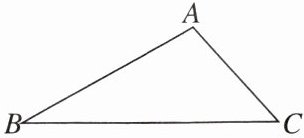
【例1】如图,已知在△ABC中,∠B= 30°,AB+BC= 12,设AB= x,△ABC的面积为S.
(1)求面积S关于x的函数表达式,并写出自变量x的取值范围.
(2)求S的最大值.
(1)求面积S关于x的函数表达式,并写出自变量x的取值范围.
(2)求S的最大值.

答案:
解:
(1)如图,过点A作AD⊥BC于点D.

在△ABD中,
∵∠ADB=90°,∠B=30°,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$x,
∴S=$\frac{1}{2}$BC·AD=$\frac{1}{2}$(12 - x)·$\frac{1}{2}$x=-$\frac{1}{4}$x² + 3x,
∴面积S关于x的函数表达式为S=-$\frac{1}{4}$x² + 3x (0 < x < 12).
(2)当x = 6时,S$_{最大}$=-$\frac{1}{4}$×6² + 3×6 = 9.
解:
(1)如图,过点A作AD⊥BC于点D.

在△ABD中,
∵∠ADB=90°,∠B=30°,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$x,
∴S=$\frac{1}{2}$BC·AD=$\frac{1}{2}$(12 - x)·$\frac{1}{2}$x=-$\frac{1}{4}$x² + 3x,
∴面积S关于x的函数表达式为S=-$\frac{1}{4}$x² + 3x (0 < x < 12).
(2)当x = 6时,S$_{最大}$=-$\frac{1}{4}$×6² + 3×6 = 9.
【变式】如图,四边形ABCD的两条对角线互相垂直,AC+BD= 16,则四边形ABCD的面积最大值是 (
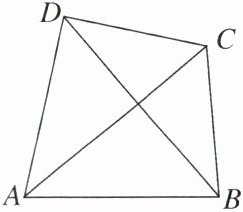
A.64
B.16
C.24
D.32
D
)
A.64
B.16
C.24
D.32
答案:
D
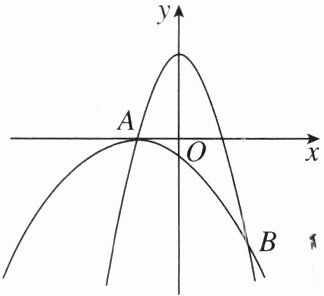
【例2】如图,两条抛物线$y_{1}= -x^{2}+4$,$y_{2}= -\frac{1}{5}x^{2}+bx+c$相交于A,B两点,点A在x轴的负半轴上,且为抛物线$y_{2}$的最高点.
(1)求抛物线$y_{2}$的函数表达式和点B的坐标.
(2)点C是抛物线$y_{1}$上A,B之间的一点,过点C作x轴的垂线交$y_{2}$于点D,求线段CD长的最大值.
(1)求抛物线$y_{2}$的函数表达式和点B的坐标.
(2)点C是抛物线$y_{1}$上A,B之间的一点,过点C作x轴的垂线交$y_{2}$于点D,求线段CD长的最大值.

答案:
解:
(1)当y$_1$ = 0,即 - x² + 4 = 0时,解得x = 2或x = - 2.又点A在x轴的负半轴上,
∴A(- 2,0).
∵点A(- 2,0)是抛物线y$_2$的最高点,
∴-$\frac{b}{2×(-\frac{1}{5})}$ = - 2,即b = -$\frac{4}{5}$.
把A(- 2,0)代入y$_2$ = -$\frac{1}{5}$x² - $\frac{4}{5}$x + c,得c = -$\frac{4}{5}$,
∴抛物线y$_2$的函数表达式为y$_2$ = -$\frac{1}{5}$x² - $\frac{4}{5}$x - $\frac{4}{5}$,y$_1$ = - x² + 4.
由$\begin{cases} y_1=-x^2+4, \\ y_2=-\frac{1}{5}x^2-\frac{4}{5}x-\frac{4}{5} \end{cases}$得$\begin{cases} x=-2, \\ y=0 \end{cases}$或$\begin{cases} x=3, \\ y=-5 \end{cases}$,
∵A(- 2,0),
∴B(3,- 5).
(2)由题意得,
CD = y$_1$ - y$_2$ = - x² + 4 - (-$\frac{1}{5}$x² - $\frac{4}{5}$x - $\frac{4}{5}$),即CD = -$\frac{4}{5}$x² + $\frac{4}{5}$x + $\frac{24}{5}$,
当x = $\frac{1}{2}$时,CD$_{最大}$=-$\frac{4}{5}$×$\frac{1}{4}$ + $\frac{4}{5}$×$\frac{1}{2}$ + $\frac{24}{5}$ = 5.
(1)当y$_1$ = 0,即 - x² + 4 = 0时,解得x = 2或x = - 2.又点A在x轴的负半轴上,
∴A(- 2,0).
∵点A(- 2,0)是抛物线y$_2$的最高点,
∴-$\frac{b}{2×(-\frac{1}{5})}$ = - 2,即b = -$\frac{4}{5}$.
把A(- 2,0)代入y$_2$ = -$\frac{1}{5}$x² - $\frac{4}{5}$x + c,得c = -$\frac{4}{5}$,
∴抛物线y$_2$的函数表达式为y$_2$ = -$\frac{1}{5}$x² - $\frac{4}{5}$x - $\frac{4}{5}$,y$_1$ = - x² + 4.
由$\begin{cases} y_1=-x^2+4, \\ y_2=-\frac{1}{5}x^2-\frac{4}{5}x-\frac{4}{5} \end{cases}$得$\begin{cases} x=-2, \\ y=0 \end{cases}$或$\begin{cases} x=3, \\ y=-5 \end{cases}$,
∵A(- 2,0),
∴B(3,- 5).
(2)由题意得,
CD = y$_1$ - y$_2$ = - x² + 4 - (-$\frac{1}{5}$x² - $\frac{4}{5}$x - $\frac{4}{5}$),即CD = -$\frac{4}{5}$x² + $\frac{4}{5}$x + $\frac{24}{5}$,
当x = $\frac{1}{2}$时,CD$_{最大}$=-$\frac{4}{5}$×$\frac{1}{4}$ + $\frac{4}{5}$×$\frac{1}{2}$ + $\frac{24}{5}$ = 5.
【例3】如图,已知抛物线$y= -x^{2}+px+q$的对称轴为直线x= -3,过其顶点M的一条直线$y= mx+n$与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN的值最小,则点P的坐标为 (
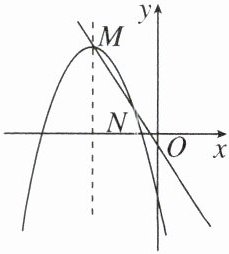
A.(0,2)
B.$\left(0,\frac{5}{3}\right)$
C.$\left(0,\frac{4}{3}\right)$
D.$\left(0,\frac{3}{2}\right)$
A
)
A.(0,2)
B.$\left(0,\frac{5}{3}\right)$
C.$\left(0,\frac{4}{3}\right)$
D.$\left(0,\frac{3}{2}\right)$
答案:
A
查看更多完整答案,请扫码查看


