第35页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
9. 如图,AB,CE是⊙O的两条直径,D是劣弧BC的中点,连结BC,DE. 若∠ABC= 34°,求∠CED的度数.


答案:
解:连结 OD,如图, $\because \angle ABC=\frac{1}{2}\angle AOC$,$\angle ABC=34^\circ$,$\therefore \angle AOC=68^\circ$.$\therefore \angle BOC=180^\circ - 68^\circ=112^\circ$.$\because$ D 是劣弧 BC 的中点,$\therefore \angle BOD=\angle COD=\frac{1}{2}\angle BOC=56^\circ$,$\therefore \angle CED=\frac{1}{2}\angle COD=28^\circ$.
$\because \angle ABC=\frac{1}{2}\angle AOC$,$\angle ABC=34^\circ$,$\therefore \angle AOC=68^\circ$.$\therefore \angle BOC=180^\circ - 68^\circ=112^\circ$.$\because$ D 是劣弧 BC 的中点,$\therefore \angle BOD=\angle COD=\frac{1}{2}\angle BOC=56^\circ$,$\therefore \angle CED=\frac{1}{2}\angle COD=28^\circ$.
解:连结 OD,如图,
 $\because \angle ABC=\frac{1}{2}\angle AOC$,$\angle ABC=34^\circ$,$\therefore \angle AOC=68^\circ$.$\therefore \angle BOC=180^\circ - 68^\circ=112^\circ$.$\because$ D 是劣弧 BC 的中点,$\therefore \angle BOD=\angle COD=\frac{1}{2}\angle BOC=56^\circ$,$\therefore \angle CED=\frac{1}{2}\angle COD=28^\circ$.
$\because \angle ABC=\frac{1}{2}\angle AOC$,$\angle ABC=34^\circ$,$\therefore \angle AOC=68^\circ$.$\therefore \angle BOC=180^\circ - 68^\circ=112^\circ$.$\because$ D 是劣弧 BC 的中点,$\therefore \angle BOD=\angle COD=\frac{1}{2}\angle BOC=56^\circ$,$\therefore \angle CED=\frac{1}{2}\angle COD=28^\circ$. 10. 如图,△ABC的顶点A,B,C均在⊙O上,连结OA,OC,若∠ABC+∠AOC= 75°,则∠OAC的度数是(
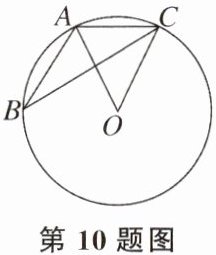
A.45°
B.50°
C.60°
D.65°
D
)
A.45°
B.50°
C.60°
D.65°
答案:
D
11. 有一题目:“已知点O为△ABC的外心,∠BOC= 130°,求∠A.”嘉嘉的解答如下:画△ABC以及它的外接圆O,连结OB,OC,如图,由∠BOC= 2∠A= 130°,得∠A= 65°. 而淇淇说:“嘉嘉考虑得不周全,还应有另一个不同的值.”下列判断正确的是( )
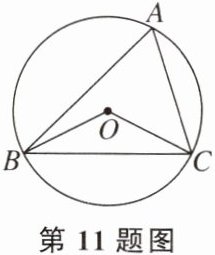
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就是65°
C.嘉嘉求的结果不对,∠A应是50°
D.两人都不对,应有3个不同值

A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就是65°
C.嘉嘉求的结果不对,∠A应是50°
D.两人都不对,应有3个不同值
答案:
A【解析】易知$\angle A\neq90^\circ$,当$\angle A$是锐角时,如嘉嘉所解,$\triangle ABC$的外心 O 在其内部,$\angle A=65^\circ$;当$\angle A$是钝角时,如图,$\triangle ABC$的外心 O 在其外部,$\because \angle1 = 2\angle A$,$\therefore \angle A=\frac{1}{2}\angle1=\frac{1}{2}×(360^\circ - 130^\circ)=115^\circ$. 故$\angle A=65^\circ$或$115^\circ$.
故$\angle A=65^\circ$或$115^\circ$.
A【解析】易知$\angle A\neq90^\circ$,当$\angle A$是锐角时,如嘉嘉所解,$\triangle ABC$的外心 O 在其内部,$\angle A=65^\circ$;当$\angle A$是钝角时,如图,$\triangle ABC$的外心 O 在其外部,$\because \angle1 = 2\angle A$,$\therefore \angle A=\frac{1}{2}\angle1=\frac{1}{2}×(360^\circ - 130^\circ)=115^\circ$.
 故$\angle A=65^\circ$或$115^\circ$.
故$\angle A=65^\circ$或$115^\circ$. 12. 如图,⊙O的半径为1,AB是⊙O的一条弦,且AB= √3,则弦AB所对的圆周角的度数为

60°或120°
.
答案:
$60°$或$120°$
13. 如图,OA,OB,OC都是⊙O的半径,∠ACB= 2∠BAC.
(1)求证:∠AOB= 2∠BOC.
(2)若AB= 4,OA= 5/2,求BC的长.
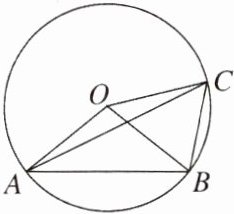
(1)求证:∠AOB= 2∠BOC.
(2)若AB= 4,OA= 5/2,求BC的长.

答案:
解:
(1)证明:$\because \angle ACB=\frac{1}{2}\angle AOB$,$\angle BAC=\frac{1}{2}\angle BOC$,$\angle ACB = 2\angle BAC$,$\therefore \angle AOB=2\angle BOC$.
(2)过点 O 作半径$OD\perp AB$于点 E,连结 DB,$\therefore AE=BE$.$\because \angle AOB=2\angle BOC$,$\angle DOB=\frac{1}{2}\angle AOB$, $\therefore \angle DOB=\angle BOC$,$\therefore BD=BC$.$\because AB = 4$,$\therefore BE=2$.在$Rt\triangle BOE$中,$\angle OEB=90^\circ$,$OA=OB=\frac{5}{2}$,$\therefore OE=\sqrt{OB^2 - BE^2}=\frac{3}{2}$,$\therefore DE=OD - OE=1$.在$Rt\triangle BDE$中,$BD=\sqrt{DE^2 + BE^2}=\sqrt{5}$,$\therefore BC=BD=\sqrt{5}$,即 BC 的长为$\sqrt{5}$.
$\therefore \angle DOB=\angle BOC$,$\therefore BD=BC$.$\because AB = 4$,$\therefore BE=2$.在$Rt\triangle BOE$中,$\angle OEB=90^\circ$,$OA=OB=\frac{5}{2}$,$\therefore OE=\sqrt{OB^2 - BE^2}=\frac{3}{2}$,$\therefore DE=OD - OE=1$.在$Rt\triangle BDE$中,$BD=\sqrt{DE^2 + BE^2}=\sqrt{5}$,$\therefore BC=BD=\sqrt{5}$,即 BC 的长为$\sqrt{5}$.
解:
(1)证明:$\because \angle ACB=\frac{1}{2}\angle AOB$,$\angle BAC=\frac{1}{2}\angle BOC$,$\angle ACB = 2\angle BAC$,$\therefore \angle AOB=2\angle BOC$.
(2)过点 O 作半径$OD\perp AB$于点 E,连结 DB,$\therefore AE=BE$.$\because \angle AOB=2\angle BOC$,$\angle DOB=\frac{1}{2}\angle AOB$,
 $\therefore \angle DOB=\angle BOC$,$\therefore BD=BC$.$\because AB = 4$,$\therefore BE=2$.在$Rt\triangle BOE$中,$\angle OEB=90^\circ$,$OA=OB=\frac{5}{2}$,$\therefore OE=\sqrt{OB^2 - BE^2}=\frac{3}{2}$,$\therefore DE=OD - OE=1$.在$Rt\triangle BDE$中,$BD=\sqrt{DE^2 + BE^2}=\sqrt{5}$,$\therefore BC=BD=\sqrt{5}$,即 BC 的长为$\sqrt{5}$.
$\therefore \angle DOB=\angle BOC$,$\therefore BD=BC$.$\because AB = 4$,$\therefore BE=2$.在$Rt\triangle BOE$中,$\angle OEB=90^\circ$,$OA=OB=\frac{5}{2}$,$\therefore OE=\sqrt{OB^2 - BE^2}=\frac{3}{2}$,$\therefore DE=OD - OE=1$.在$Rt\triangle BDE$中,$BD=\sqrt{DE^2 + BE^2}=\sqrt{5}$,$\therefore BC=BD=\sqrt{5}$,即 BC 的长为$\sqrt{5}$. 查看更多完整答案,请扫码查看


