《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

【例1】如图,抛物线$ y= ax^{2}+bx+c $与x轴相交于点$ A(-1,0),B(2,0) $.
(1)方程$ ax^{2}+bx+c= 0 $的解为$x_{1}=-1$,$x_{2}=2$.
(2)不等式$ ax^{2}+bx+c＞0 $的解集为$-1＜x＜2$.
(3)不等式$ ax^{2}+bx+c\leq0 $的解集为$x\leqslant -1$或$x\geqslant 2$.

答案：
(1)$x_{1}=-1$,$x_{2}=2$　
(2)$-1＜x＜2$　
(3)$x\leqslant -1$或$x\geqslant 2$

【变式】如图,抛物线$ y= ax^{2}+bx+c(a\neq0) $与x轴交于点$ A(-1,0) $,顶点坐标为$ (1,n) $,与y轴的交点在$ (0,2) 和 (0,3) $两点之间(包含端点).下列结论中正确的是(①③④)
①不等式$ ax^{2}+c＜-bx 的解集为 x＜-1 或 x＞3 $；
②$ 9a^{2}-b^{2}＜0 $；
③一元二次方程$ cx^{2}+bx+a= 0 的两个根分别为 x_{1}= \frac{1}{3},x_{2}= -1 $；
④$ 6\leq3n-2\leq10 $.

A.①②③
B.①②④
C.②③④
D.①③④

答案： D　[解析]
∵顶点坐标为$(1,n)$,
∴$-\dfrac{b}{2a}=1$，即$b=-2a$。
∵与$x$轴交于点$A(-1,0)$，
∴$a - b + c = 0$，
∴$c = -3a$。
∵对称轴为直线$x = 1$，且抛物线经过点$(-1,0)$，
∴抛物线与$x$轴的另一个交点为$(3,0)$。
∵抛物线开口向下，
∴不等式$ax^{2}+bx+c＜0$的解集为$x ＜ -1$或$x ＞ 3$，即不等式$ax^{2}+c ＜ -bx$的解集为$x ＜ -1$或$x ＞ 3$，
　故①正确；
∵$9a^{2}-b^{2}=9a^{2}-(-2a)^{2}=5a^{2}＞0$，
　故②不正确；
∵一元二次方程$cx^{2}+bx+a=0$可化为$-3ax^{2}-2ax+a=0$，即$3x^{2}+2x - 1 = 0$，
∴方程的根为$x_{1}=\dfrac{1}{3}$，$x_{2}=-1$，
　故③正确；
∵抛物线与$y$轴的交点在$(0,2)$和$(0,3)$两点之间，
∴$2\leqslant c\leqslant 3$。
∵顶点坐标为$(1,n)$，
∴$n = -4a$。
∵$c = -3a$，
∴$n=\dfrac{4}{3}c$，
∴$\dfrac{8}{3}\leqslant n\leqslant 4$，
∴$6\leqslant 3n - 2\leqslant 10$，故④正确；

【例2】已知函数$ y_{1}= x^{2}-(m+2)x+2m+3 $,$ y_{2}= nx+k-2n $(m,n,k为常数且$ n\neq0 $).
(1)若函数$ y_{1} 的图象经过 A(2,5),B(-1,3) $两个点中的一个点,求该函数的表达式.
(2)若函数$ y_{1},y_{2} $的图象始终经过同一定点M.
①求点M的坐标和k的值.
②若$ m\leq2 $,当$ -1\leq x\leq2 $时,总有$ y_{1}\leq y_{2} $,求$ m+n $的取值范围.

答案：

(1)对于函数$y_{1}=x^{2}-(m + 2)x + 2m + 3$，当$x = 2$时，$y = 3$，
∴点$A$不在该函数图象上。
　把$B(-1,3)$代入$y_{1}=x^{2}-(m + 2)x + 2m + 3$，
　得$3 = 1 + 3m + 5$，解得$m = -1$，
∴该函数的表达式为$y_{1}=x^{2}-x + 1$。
(2)①
∵函数$y_{1}$经过定点$(2,3)$，对于函数$y_{2}=nx + k - 2n$，当$x = 2$时，$y_{2}=k$，
∴当$k = 3$时，两个函数的图象始终过同一定点$M(2,3)$。
　②
∵$m\leqslant 2$，
∴函数$y_{1}$图象的对称轴即直线$x=\dfrac{m + 2}{2}\leqslant 2$，
∴函数$y_{1}$图象的对称轴在定点$M(2,3)$的左侧，如图，由题意，当$1+(m + 2)+2m + 3\leqslant -n + 3 - 2n$ 时，满足当$-1\leqslant x\leqslant 2$时，总有$y_{1}\leqslant y_{2}$，
∴$3m + 3n\leqslant -3$，
∴$m + n\leqslant -1$。

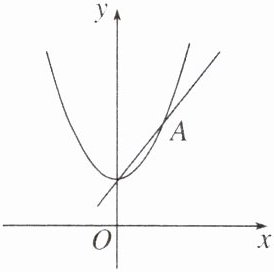
【变式1】如图,二次函数$ y= ax^{2}+c $的图象与一次函数 y= kx+c 的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式$ ax^{2}+c＜kx+c $的解集为$0 ＜ x ＜ 1$.

答案： $0 ＜ x ＜ 1$

【变式2】若二次函数$ y= x^{2}+bx-5 $图象的对称轴为直线 $x= 2 $,则关于x的方程$ x^{2}+bx-5= 2x-13 $的解为$x = 2$或$x = 4$.

答案： $x = 2$或$x = 4$