第70页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
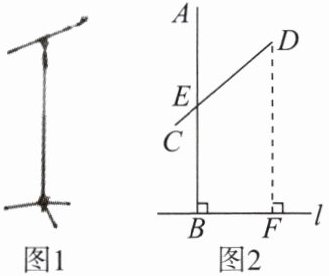
【例1】图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED= 48°,BE= 110 cm,DE= 80 cm,求活动杆端点D离地面的高度DF.(结果精确到1 cm,参考数据:sin 48°≈0.74,cos 48°≈0.67,tan 48°≈1.11)

答案:
解:如图,过点D作DG⊥AE于点G,得矩形GBFD,
∴DF=GB.
在Rt△GDE中,DE=80cm,∠GED =48°,
∴GE=DE×cos 48°≈80×0.67=53.6(cm),
∴GB=GE+BE≈53.6+110=163.6≈164(cm).
∴DF=GB≈164cm.
答:活动杆端点D离地面的高度DF为164cm.

解:如图,过点D作DG⊥AE于点G,得矩形GBFD,
∴DF=GB.
在Rt△GDE中,DE=80cm,∠GED =48°,
∴GE=DE×cos 48°≈80×0.67=53.6(cm),
∴GB=GE+BE≈53.6+110=163.6≈164(cm).
∴DF=GB≈164cm.
答:活动杆端点D离地面的高度DF为164cm.

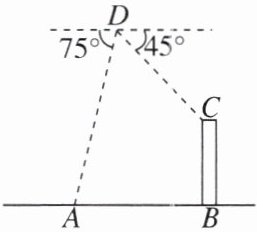
【变式】如图,某无人机爱好者在一小区外操控无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为70米,此时无人机D距地面AB的高度为74.6米,求小区楼房BC的高度.(参考数据:sin 75°≈0.97,cos 75°≈0.26,tan 75°≈3.73)

答案:
解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,如图所示,
则∠DAE=75°,∠DCF=45°,
∴△CDF是等腰直角三角形,
∴DF=CF.
在Rt△ADE中,tan∠DAE=$\frac{DE}{AE}$,
∴AE=$\frac{DE}{\tan75^\circ}$≈$\frac{74.6}{3.73}$=20(米),
∴BE=AB - AE≈70 - 20=50(米).
∵四边形BCFE是矩形,
∴CF=BE≈50米.
∴DF=CF≈50米,
∴BC=EF=DE - DF≈74.6 - 50=24.6(米).
答:小区楼房BC的高度约为24.6米.

解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,如图所示,
则∠DAE=75°,∠DCF=45°,
∴△CDF是等腰直角三角形,
∴DF=CF.
在Rt△ADE中,tan∠DAE=$\frac{DE}{AE}$,
∴AE=$\frac{DE}{\tan75^\circ}$≈$\frac{74.6}{3.73}$=20(米),
∴BE=AB - AE≈70 - 20=50(米).
∵四边形BCFE是矩形,
∴CF=BE≈50米.
∴DF=CF≈50米,
∴BC=EF=DE - DF≈74.6 - 50=24.6(米).
答:小区楼房BC的高度约为24.6米.

【例2】如图,在Rt△ABC中,∠BAC= 90°,AD⊥BC于点D,则下列结论中不正确的是(
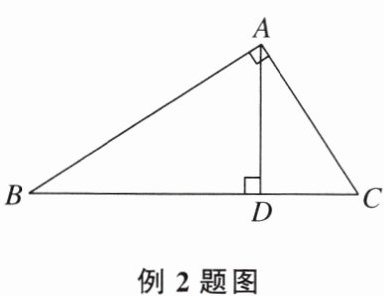
A.$\sin B= \frac{AD}{AB}$
B.$\sin B= \frac{AC}{BC}$
C.$\sin B= \frac{AD}{AC}$
D.$\sin B= \frac{CD}{AC}$
C
)
A.$\sin B= \frac{AD}{AB}$
B.$\sin B= \frac{AC}{BC}$
C.$\sin B= \frac{AD}{AC}$
D.$\sin B= \frac{CD}{AC}$
答案:
C
【变式】如图,AB是⊙O的直径,$\overset{\frown}{AD}= \overset{\frown}{DE}$,AB= 5,BD= 4,则$\sin\angle ECB= $
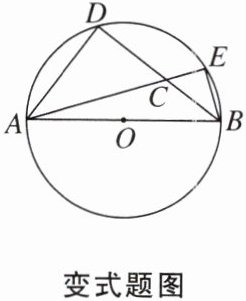
$\frac{4}{5}$
.
答案:
$\frac{4}{5}$
查看更多完整答案,请扫码查看


