《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

8. 在△ABC 与△A'B'C'中,有下列条件：①$\frac{AB}{A'B'}= \frac{BC}{B'C'}$；②$\frac{AC}{A'C'}= \frac{BC}{B'C'}$；③∠A= ∠A'；④∠C= ∠C'. 如果从中任取两个条件组成一组,那么能判定△ABC∽△A'B'C'的共有3组.

答案： 3

9. 如图,△ABC 的三边长分别为 AB= 3 cm,BC= 3.5 cm,CA= 2.5 cm,△DEF 的三边长分别为 DE= 3.6 cm,EF= 4.2 cm,FD= 3 cm. △ABC 与△DEF 是否相似？为什么？

答案： 解：△ABC∽△DEF. 理由如下：
∵$\frac{AB}{DE}=\frac{3}{3.6}=\frac{5}{6}$，$\frac{BC}{EF}=\frac{3.5}{4.2}=\frac{5}{6}$，$\frac{CA}{FD}=\frac{2.5}{3}=\frac{5}{6}$，
∴$\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$，
∴△ABC∽△DEF.

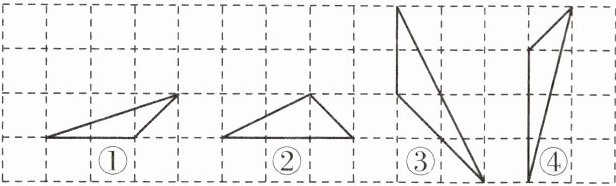
10. 如图所示,网格中相似的两个三角形是①③.(填序号)

答案： ①③ 【解析】设题图中小正方形的边长为 1，则图形①的三边为 2，$\sqrt{10}$，$\sqrt{2}$；
图形②的三边为 3，$\sqrt{5}$，$\sqrt{2}$；
图形③的三边为 2，$2\sqrt{2}$，$2\sqrt{5}$；
图形④的三边为 3，$\sqrt{2}$，$\sqrt{17}$.
∵$\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$，$\frac{\sqrt{10}}{2\sqrt{5}}=\frac{\sqrt{2}}{2}$，
∴①与③相似.

11. 在每个小正方形的边长为 1 的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形. 如图,已知 Rt△ABC 是 6×6 网格图形中的格点三角形,则该图中所有与 Rt△ABC 相似的格点三角形中,面积最大的三角形的斜边长是______.

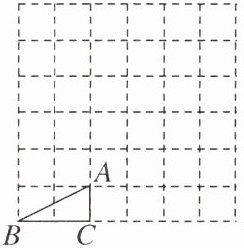
答案：
$5\sqrt{2}$ 【解析】
∵在 Rt△ABC 中，AC=1，BC=2，
∴AB=$\sqrt{5}$，AC：BC=1：2，
∴与 Rt△ABC 相似的格点三角形的两直角边长的比值为 1：2
若该三角形最短边长为 4，则另一直角边长为 8，但在 6×6 网格图形中，最长线段为$6\sqrt{2}$，此时画出的直角三角形为等腰直角三角形，从而画不出端点都在格点上且长为 8 的线段，故最短直角边长应小于 4，在图中尝试，可画出 DE=$\sqrt{10}$，EF=$2\sqrt{10}$，DF=$5\sqrt{2}$的三角形，
∵$\frac{\sqrt{10}}{1}=\frac{2\sqrt{10}}{2}=\frac{5\sqrt{2}}{\sqrt{5}}=\sqrt{10}$，
∴△ABC∽△DFE，
∴∠DEF=∠C=90°，此时△DEF 的面积为$\sqrt{10}$×$2\sqrt{10}$÷2=10，△DEF 为面积最大的三角形，其斜边长为$5\sqrt{2}$.

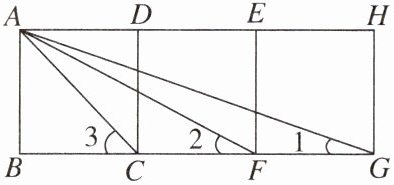
12. 如图,四边形 ABCD,DCFE,EFGH 是三个边长为 1 的正方形.
(1)求证：△ACF∽△GCA.
(2)求∠1+∠2+∠3 的度数.

答案： 解：
(1)证明：
∵AB=BC=CF=FG=1，
∴BF=2，BG=3.
由勾股定理得 AC=$\sqrt{2}$，AF=$\sqrt{5}$，AG=$\sqrt{10}$，
∵$\frac{CF}{AC}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$，$\frac{AC}{CG}=\frac{\sqrt{2}}{2}$，$\frac{FA}{AG}=\frac{\sqrt{5}}{\sqrt{10}}=\frac{\sqrt{2}}{2}$，
∴$\frac{CF}{CA}=\frac{CA}{CG}=\frac{FA}{AG}$，
∴△ACF∽△GCA.
(2)由
(1)得∠1=∠FAC.
∵四边形 ABCD 是正方形，
∴∠3=45°，
∴∠2+∠FAC=∠3=45°，
∴∠1+∠2=45°，
∴∠1+∠2+∠3=90°.

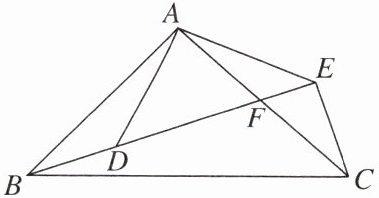
13. 如图,点 B,D,E 在一条直线上,BE 与 AC 相交于点 F,$\frac{AB}{AD}= \frac{BC}{DE}= \frac{AC}{AE}$.
(1)求证：∠BAD= ∠CAE.
(2)连结 EC,求证：△ABD∽△ACE.

答案： 证明：
(1)
∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAC - ∠DAF=∠DAE - ∠DAF，
即∠BAD=∠CAE.
(2)由
(1)知∠BAD=∠CAE.
∵$\frac{AB}{AD}=\frac{AC}{AE}$，
∴$\frac{AB}{AC}=\frac{AD}{AE}$，
∴△ABD∽△ACE.