《2025年精彩练习就练这一本九年级数学全一册浙教版评议教辅》

【例1】数轴可以度量圆的直径,则下图中的圆形图片的直径是(B)

A.5－1
B.5－(－1)
C.－5－1
D.－5－(－1)

答案： B

【变式】“车轮为什么都做成圆形？”下面解释最合理的是(D)
A.圆形是轴对称图形
B.圆形特别美观大方
C.圆形是曲线图形
D.从圆心到圆上任意一点的距离都相等

答案： D

【例2】如图,在△ABC中,∠CAB＝65°,将△ABC在平面内绕点A旋转到△AB'C'的位置,使CC'//AB,则旋转角的度数为(C)

A.30°
B.40°
C.50°
D.65°

答案： C

【变式】如图,在平面直角坐标系中,△ABC的顶点都在格点(每个小正方形的边长均为1个单位长度,小正方形的顶点称为格点)上,点A,B,C的坐标分别为A(－3,2),B(0,1),C(－2,0),将△ABC绕坐标平面内某点旋转一定的角度,得到△A'B'C',点A,B,C的对应点分别为A',B',C',若点B'的坐标为(3,0),则旋转中心的坐标为( )


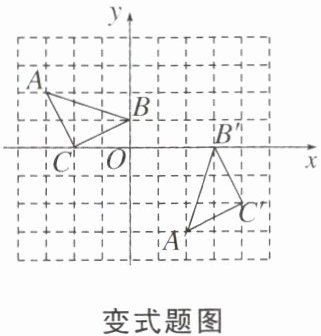
A.(2,1)
B.(2,2)
C.(2,0)
D.(－1,0)

答案：
B [解析]如图所示,
　　　　　　　
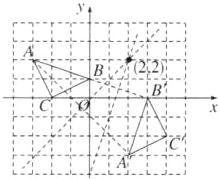
∴旋转中心的坐标为(2,2)．

【例3】如图,⊙O的两条弦AB,CD互相垂直且相交于点P,OE⊥AB,OF⊥CD,垂足分别为E,F,$\widehat{AC}= \widehat{BD}$.求证：四边形OEPF是正方形.

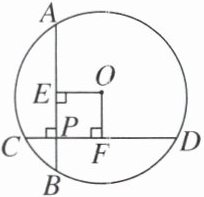
答案： 证明:
∵$\stackrel{\frown }{AC}=\stackrel{\frown }{BD}$，
∴$\stackrel{\frown }{AC}+\stackrel{\frown }{BC}=\stackrel{\frown }{BD}+\stackrel{\frown }{BC}$，即$\stackrel{\frown }{AB}=\stackrel{\frown }{CD}$，
∴AB=CD．
　又
∵OE⊥AB，OF⊥CD，
∴OE=OF，∠OEP=∠OFP=90°．
∵AB⊥CD，
∴∠EPF=90°=∠OEP=∠OFP，
∴四边形OEPF是矩形
　　又
∵OE=OF，
∴矩形OEPF是正方形．

【变式】一条排水管的截面如图所示,已知排水管的截面圆的半径OB＝10 dm,水面宽AB是16 dm,则截面水深CD是(B)

A.3 dm
B.4 dm
C.5 dm
D.6 dm

答案： B