第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
10. (1)观察下列各数:1,$\frac{4}{3}$,$\frac{9}{7}$,$\frac{16}{15}$,…,按照这样的规律,第 5 个数为
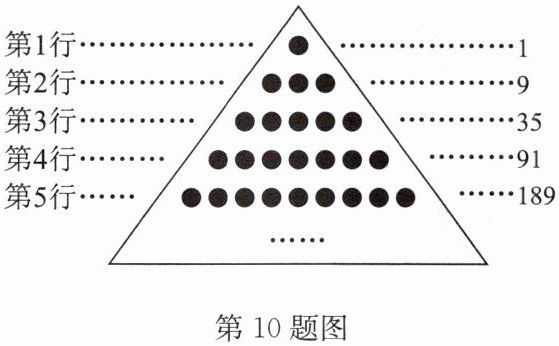
(2)如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右按从小到大的顺序排列,且相邻两个点所表示的数相差 1,每行数的和等于右边相应的数字.那么表示 2025 的点在第
$\frac{25}{31}$
;(2)如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右按从小到大的顺序排列,且相邻两个点所表示的数相差 1,每行数的和等于右边相应的数字.那么表示 2025 的点在第
45
行,从左向右第89
个位置.
答案:
(1)$\frac{25}{31}$
(2)45 89
(1)$\frac{25}{31}$
(2)45 89
11. (1)某校暑假组织该校“三好学生”去北京旅游,由 3 名老师带队,甲旅行社说:“如果带队老师买全票,则学生可享受半价优惠”,乙旅行社说:“包括带队老师在内全部按全票价的 6 折优惠”.若一个人的全票价是 800 元,设学生人数为 x,分别计算两家旅行社的费用;
(2)一种商品每件成本为 a 元,原来按成本增加 20%定价,现在由于库存积压进行降价,按原价的 85%出售.原来每件售价多少元? 现在每件售价多少元? 现在每件盈利多少元?
(2)一种商品每件成本为 a 元,原来按成本增加 20%定价,现在由于库存积压进行降价,按原价的 85%出售.原来每件售价多少元? 现在每件售价多少元? 现在每件盈利多少元?
答案:
解:
(1)选择甲旅行社的费用为 $3×800 + 800x×0.5=(2400 + 400x)$ 元;选择乙旅行社的费用为 $800×(x + 3)×0.6=(480x + 1440)$ 元。
(2)原来每件售价为 $(1 + 20\%)a = 1.2a$ (元),现在每件售价为 $1.2a×85\% = 1.02a$ (元),现在每件盈利 $1.02a - a = 0.02a$ (元)。
(1)选择甲旅行社的费用为 $3×800 + 800x×0.5=(2400 + 400x)$ 元;选择乙旅行社的费用为 $800×(x + 3)×0.6=(480x + 1440)$ 元。
(2)原来每件售价为 $(1 + 20\%)a = 1.2a$ (元),现在每件售价为 $1.2a×85\% = 1.02a$ (元),现在每件盈利 $1.02a - a = 0.02a$ (元)。
12. 观察下列等式:
①$2^{2}-2^{1}= 4-2= 2^{1}$;
②$2^{3}-2^{2}= 8-4= 2^{2}$;
③$2^{4}-2^{3}= 16-8= 2^{3}$;
④______;
……
(1)请写出第④个等式:
(2)根据你发现的规律,用含字母 n 的式子表示第 n 个等式:
(3)请利用上述规律计算:$2^{1}+2^{2}+…+2^{100}$.
①$2^{2}-2^{1}= 4-2= 2^{1}$;
②$2^{3}-2^{2}= 8-4= 2^{2}$;
③$2^{4}-2^{3}= 16-8= 2^{3}$;
④______;
……
(1)请写出第④个等式:
$2^{5}-2^{4}=32 - 16 = 2^{4}$
;(2)根据你发现的规律,用含字母 n 的式子表示第 n 个等式:
$2^{n + 1}-2^{n}=2^{n}$
;(3)请利用上述规律计算:$2^{1}+2^{2}+…+2^{100}$.
解:因为 $2^{2}-2^{1}=4 - 2 = 2^{1}$,$2^{3}-2^{2}=8 - 4 = 2^{2}$,…,$2^{101}-2^{100}=2^{100}$,所以原式 $=2^{2}-2^{1}+2^{3}-2^{2}+\cdots+2^{101}-2^{100}=2^{101}-2$。
答案:
(1)$2^{5}-2^{4}=32 - 16 = 2^{4}$;
(2)$2^{n + 1}-2^{n}=2^{n}$;
(3)解:因为 $2^{2}-2^{1}=4 - 2 = 2^{1}$,$2^{3}-2^{2}=8 - 4 = 2^{2}$,…,$2^{1001}-2^{1000}=2^{1000}$,所以原式 $=2^{2}-2^{1}+2^{3}-2^{2}+\cdots+2^{1001}-2^{1000}=2^{1001}-2$。
(1)$2^{5}-2^{4}=32 - 16 = 2^{4}$;
(2)$2^{n + 1}-2^{n}=2^{n}$;
(3)解:因为 $2^{2}-2^{1}=4 - 2 = 2^{1}$,$2^{3}-2^{2}=8 - 4 = 2^{2}$,…,$2^{1001}-2^{1000}=2^{1000}$,所以原式 $=2^{2}-2^{1}+2^{3}-2^{2}+\cdots+2^{1001}-2^{1000}=2^{1001}-2$。
查看更多完整答案,请扫码查看


