《2025年初中必刷题七年级数学上册北师大版》

1 [2025甘肃武威质检]若$m = n$,则下列等式中错误的是( )

A.$-4m = -4n$
B.$1 + m = 1 + n$
C.$\frac{m}{2} = \frac{n}{2}$
D.$3 - m = 3 + n$

答案： 1. D　[解析]A选项，等式的两边同时乘−4，等式成立，正确，不符合题意；B选项，等式的两边同时加1，等式成立，正确，不符合题意；C选项，等式的两边同时乘$\frac{1}{2}$，等式成立，正确，不符合题意；D选项，$3 - m = 3 + n$，则$ - m = n$，与$m = n$矛盾，不正确，符合题意。故选D。

2 [2025天津河北区期末]下面利用等式的基本性质对等式进行的变形,错误的是( )

A.若$a = 5$,则$a^{2} = 5a$
B.$bm = bn$,则$m = n$
C.若$\frac{m}{b} = \frac{n}{b}$,则$m = n$
D.若$-\frac{x}{2} = 8$,则$x = -16$

答案： 2. B　[解析]若$a = 5$，则$a^{2} = 5a$，A正确，不符合题意；$bm = bn$，则$m = n$，前提是$b≠0$，B错误，符合题意；若$\frac{m}{b} = \frac{n}{b}$，则$m = n$，C正确，不符合题意；若$-\frac{x}{2} = 8$，则$x = - 16$，D正确，不符合题意。故选B。

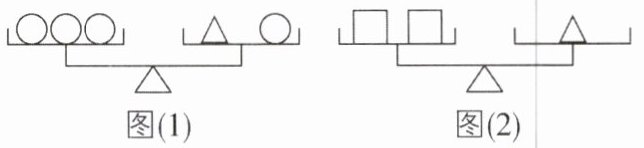
3 [2024广西桂林质检]设“$◯$”“$\triangle$”“$□$”表示三种不同的物体,现用天平称了两次,天平都处于平衡状态(如图),则下列式子中“$□$”和“$◯$”的关系正确的是( )


A.$□ = ◯$
B.$□ = 2◯$
C.$2□ = 3◯$
D.$3□ = 4◯$

答案：
3. A　[解析]
观察题图
(1)
等式的基本性质1
$3○ = △ + ○$ $2○ = △$
观察题图
(2) $2□ = △$
等式的基本性质2 等量代换
$○ = □$ $2○ = 2□$

4 [2024广东广州天河区期中]如果$3x = 2x + 6$,那么$3x$______$= 6$。

答案： 4. -2x　[解析]由题可知，$3x = 2x + 6$的两边都减$2x$，得$3x - 2x = 6$。故答案为$-2x$。

5 [2025浙江宁波期末]下列方程的变形正确的是( )

A.$2x = 1$,变形为$x = 2$

B.$x + 5 = 3 - 3x$,变形为$4x = 2$
C.$\frac{2}{3}x - 1 = 2$,变形为$2x - 3 = 2$
D.$3x - 6 = 0$,变形为$3x = 6$

答案： 5. D　[解析]因为$2x = 1$，变形为$x = 0.5$，所以选项A不符合题意；因为$x + 5 = 3 - 3x$，变形为$4x = - 2$，所以选项B不符合题意；因为$\frac{2}{3}x - 1 = 2$，变形为$2x - 3 = 6$，所以选项C不符合题意；因为$3x - 6 = 0$，变形为$3x = 6$，所以选项D符合题意。故选D。

6 (1)在等式$-3x + 2 = 5$的两边都______得到等式$-3x = 3$,这是根据______；
(2)在等式$7x = 6x + 1$的两边都______得到等式$x = 1$,这是根据______；
(3)在等式$-4x = \frac{1}{2}$的两边都______得到等式$x = -\frac{1}{8}$,这是根据______。

答案： 6.
(1)减2 等式的基本性质1
(2)减6x 等式的基本性质1
(3)除以−4 等式的基本性质2　[解析]
(1)在等式$-3x + 2 = 5$的两边都减2，得到等式$-3x = 3$，这是根据等式的基本性质1。
(2)在等式$7x = 6x + 1$的两边都减6x 列方程时必须得到等式$x = 1$，这是根据等式的基本性质1。
(3)在等式$-4x = \frac{1}{2}$的两边都除以−4得到等式$x = -\frac{1}{8}$，这是根据等式的基本性质2。

7 运用等式的基本性质解下列方程：
(1)$x + 1 = \frac{1}{2}$；
(2)$3x = 2x + 12$；
(3)$\frac{x}{2} - 3 = 5$(需检验)；
(4)$\frac{2}{3}x + 1 = -5$(需检验)。

答案： 7. [解]
(1)方程两边都减1，得$x = -\frac{1}{2}$。
(2)方程两边都减$2x$，得$x = 12$。
(3)方程两边都加3，得$\frac{x}{2} = 8$。方程两边都乘2，得$x = 16$。
检验：当$x = 16$时，左边 = 5 = 右边，故$x = 16$是原方程的解。
(4)方程两边都减1，得$\frac{2}{3}x = - 6$。方程两边都除以$\frac{2}{3}$，得$x = - 9$。
检验：当$x = - 9$时，左边 = - 5 = 右边，故$x = - 9$是原方程的解。

8 小明学习了等式的基本性质后,做了以下结论很荒谬的推理：
如果$a = b$,那么$2a = 2b$,$3a = 3b$,①
则$2a + 3b = 3a + 2b$,②
则$2a - 2b = 3a - 3b$,③
则$2(a - b) = 3(a - b)$,④
则$2 = 3$。⑤
以上推理错误步骤的序号是什么？说明它出错的理由。

答案： 8. [解]根据等式的基本性质可知，错误在第⑤步。理由：因为$a = b$，所以$a - b = 0$，所以等式两边不能都除以$(a - b)$，所以得到$2 = 3$是错误的。