《2025年初中必刷题七年级数学上册北师大版》

1[2025山东淄博质检,中]如图,往一个密封的正方体容器内持续注入一些水,注水的过程中,可将容器任意放置,水平面形状不可能是( )


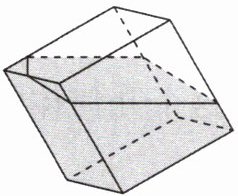
A.三角形
B.正方形
C.六边形
D.七边形

答案： D 【解析】正方体容器有六个面,注水的过程中,可将容器任意放置,水平面最多与正方体容器的六个面相交得六边形,最少与正方体容器的三个面相交得三角形,所得水平面形状可能是三角形、四边形、五边形和六边形,不可能出现七边形. 故选 D.

2[2025广东深圳期中,中]一个物体的外形是长方体(如图(1)),其内部构造不祥.用平面横向自下而上截这个物体时,得到了一组截面,截面形状如图(2)所示,则这个长方体的内部构造可能是( )
A. 圆柱
B. 球
C. 圆锥
D. 圆柱或球

答案： C 【解析】通过观察截面可以发现,内部的圆由大圆逐渐变成小圆,最后变成点,所以这个长方体的内部构造可能是圆锥. 故选 C.

3[中]一个正方体切掉一个角后,剩下的几何体顶点的个数是( )

A.7或8
B.8或9
C.7或8或9
D.7或8或9或10

答案：
D 【解析】如图
(1)，剩下的几何体有 7 个顶点;如图
(2)，剩下的几何体有 8 个顶点;如图
(3)，剩下的几何体有 9 个顶点;如图
(4)，剩下的几何体有 10 个顶点. 故选 D.

4[2024江苏镇江京口区期末,较难]用一个平面截一个直n棱柱,得到的截面边数最多是8条,且这个n棱柱的每个侧面都是正方形,正方形的面积为4,则这个n棱柱的棱长之和为______.

答案： 36 【解析】因为用一个平面截一个直 n 棱柱,得到的截面边数最多是 8 条,所以这个直 n 棱柱有 8 个面,所以这个几何体是六棱柱. 因为这个棱柱的每个侧面都是正方形,正方形的面积为 4,所以这个六棱柱的所有棱长都相等,且棱长为 2,所以六棱柱的棱长之和为 2×6×3 = 36,故答案为 36.

5[较难]如图,一个正方体形状的木块,棱长为2米.若沿正方体的三个方向分别锯成3份、4份和5份,得到若干个大大小小的长方体木块,则所有的长方体木块的表面积和是______平方米.

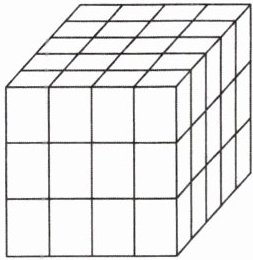
答案： 96 【解析】沿水平方向将它锯成 3 片,是锯了 2 次;同理,每片又锯成 4 长条,是锯了 3 次;接着每条又锯成 5 小块,是锯了 4 次,所以一共锯了 2 + 3 + 4 = 9(次),每锯一次表面积增加 2×2×2 = 8(平方米),所以所有的长方体木块的表面积和是 6×2×2 + 9×8 = 96(平方米). 故答案为 96.

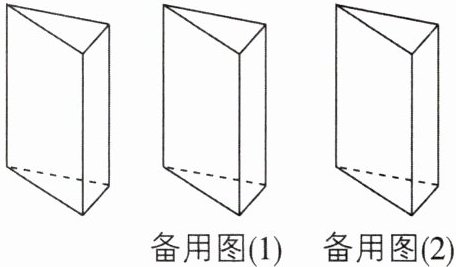
6[中]如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.
(1)所得的截面能否是三个与该三棱柱的底面大小相同的三角形？若能,画图说明你的截法.
(2)截得的截面能否是三个长相等的长方形？若能,画图说明你的一种截法.
(3)截得的截面能否是梯形？若能,画图说明你的一种截法.

答案： 【解】
(1)能. 如图
(1)所示.
(2)能. 如图
(2)所示. (截法不唯一)
(3)能. 如图
(3)所示. (截法不唯一)

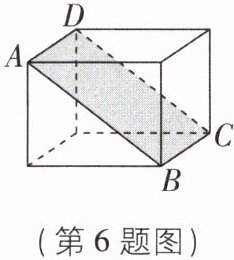
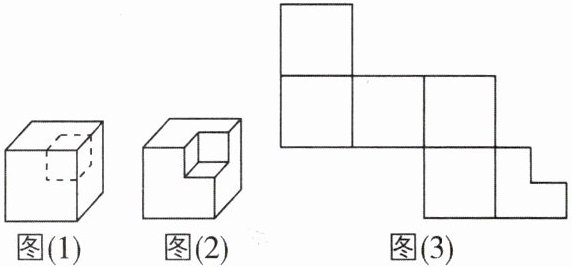
7[2024广东揭阳期中,较难]如图(1),从大正方体上截去一个小正方体之后,可以得到图(2)的几何体.
(1)设原大正方体的表面积为S,图(2)中几何体的表面积为$S_1,$那么$S_1$与S的大小关系是______.
$A. S_1＞S$
$B. S_1= S$
$C. S_1＜S$
D. 无法确定
(2)小明说：“设图(1)中大正方体各棱的长度之和为l,图(2)中几何体各棱的长度之和为$l_1,$那么$l_1$比l正好多出大正方体3条棱的长度.”你认为这句话对吗？为什么？
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图(3)是图(2)中几何体的表面展开图吗？如有错误,请予修正.

答案：
【解】
(1)由题图可得 S₁ = S. 故答案为 B.
(2)不对. 理由:设大正方体棱长为 y,被截去的小正方体棱长为 x,那么 l₁ - l = 6x. 只有当 6x = 3y,即 2x = y 时,才有 l₁比 l 正好多出大正方体 3 条棱的长度,所以小明说的话不对.
(3)不是. 修正后如图所示: