《2025年初中必刷题七年级数学上册北师大版》

1 已知$a + b = 3$,$c - d = - 2$,则$(b + c)-(d - a)$的值为( )

A.5
B.- 5
C.1
D.- 1

答案： C 【解析】因为a+b=3,c-d=-2,所以(b+c)-(d-a)=b+c-d+a=(a+b)+(c-d)=3+(-2)=1.故选C.

2 [2025广东深圳期末]有一道题是一个多项式减去$x$,小强误当成加法计算,结果得到$x^{2}+14x - 6$,这道题正确的结果应该是( )

A.$x^{2}+12x - 6$
B.$x^{2}+13x - 6$
C.$x^{2}+15x - 6$
D.$x^{2}+16x - 6$

答案： A 【解析】由题意可得，这个多项式为(x²+14x-6)-x=x²+14x-6-x=x²+13x-6，所以这道题正确的结果为(x²+13x-6)-x=x²+13x-6-x=x²+12x-6.故选A.

3 数学课上,老师设计了一个游戏：若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”. 甲、乙、丙三位同学各有一张写有多项式的卡片,下面是甲、乙、丙三位同学的对话.

甲：我的多项式是$2x^{2}-3x - 2$.
乙：我的多项式是$3x^{2}-x + 1$.
丙：我的多项式和你们两个的多项式是“友好多项式”.
在多项式①$-x^{2}-2x - 3$,②$x^{2}+2x + 3$,③$5x^{2}-4x + 1$,④$5x^{2}-4x - 1$中,丙同学卡片上的多项式可以是____.(填序号)

答案： ①或②或④ 【解析】由题意可知，这个多项式可以是2x²-3x-2-(3x²-x+1)=2x²-3x-2-3x²+x-1=-x²-2x-3，或2x²-3x-2+(3x²-x+1)=2x²-3x-2+3x²-x+1=5x²-4x-1，或3x²-x+1-(2x²-3x-2)=3x²-x+1-2x²+3x+2=x²+2x+3.

4 已知$A = 3x^{2}-2xy + y^{2}$,$B = 2x^{2}+3xy - 4y^{2}$,求：
(1)$A - 2B$；(2)$2A + B$.

答案： 【解】
(1)A - 2B=(3x²-2xy+y²)-2(2x²+3xy-4y²)=3x²-2xy+y²-4x²-6xy+8y²=-x²-8xy+9y².
(2)2A + B=2(3x²-2xy+y²)+(2x²+3xy-4y²)=6x²-4xy+2y²+2x²+3xy-4y²=8x²-xy-2y².

5 三角形的周长为$a(a ＞ 4)$,它的一边长是周长的$\frac{1}{4}$,另一边长是周长与4的差的一半,则第三边的长为( )

A.$\frac{1}{2}(a - 4)$
B.$\frac{1}{4}a - 2$
C.$\frac{1}{4}a + 2$
D.$\frac{3}{4}a + 2$

答案： C 【解析】由题意得第三边的长为a-$\frac{1}{4}$a-$\frac{1}{2}$(a-4)=a-$\frac{1}{4}$a-$\frac{1}{2}$a+2=$\frac{1}{4}$a+2.

6 [2025山东青岛期末]如图,两个正方形的面积分别为26,9,两阴影部分的面积分别为$a$,$b(a ＞ b)$,则$a - b= $( )


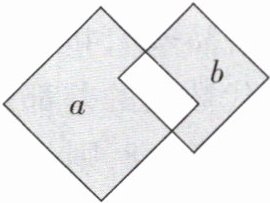
A.4
B.9
C.17
D.25

答案： C 【解析】设空白部分的面积为x.由题意可得a+x=26,b+x=9,所以(a+x)-(b+x)=26-9，所以a+x-b-x=17，所以a-b=17.故选C.

7 [2025陕西西安期末]小艾同学某月开始阅读必读名著,已知她第一周阅读《朝花夕拾》$(3a - b)$页,《西游记》$(3b - a)$页,则她第一周阅读这两本书共____页.

答案： (2a+2b) 【解析】由题意得(3a-b)+(3b-a)=3a-b+3b-a=(2a+2b)页.故答案为(2a+2b).

8 [2025河北石家庄期末]三个连续的偶数,设最小的一个为$2n$,那么它们的和可表示为____.

答案： 6n+6 【解析】另外两个偶数分别为2n+2，2n+4，所以2n+(2n+2)+(2n+4)=2n+2n+2+2n+4=6n+6.故答案为6n+6.

9 [2025四川成都质检]二路公交车上原有$(3m - n)$人,中途有一半人下车,又有若干人上车,此时车上共有乘客$(8m - 5n)$人.
(1)请问中途上车的乘客有多少人？
(2)当$m = 10$,$n = 8$时,中途上车的乘客有多少人？

答案： 【解】
(1)由题意得(8m-5n)-(3m-n)+$\frac{1}{2}$(3m-n)=8m-5n-3m+n+$\frac{3}{2}$m-$\frac{1}{2}$n=$\frac{13}{2}$m-$\frac{9}{2}$n，即中途上车的乘客有($\frac{13}{2}$m-$\frac{9}{2}$n)人.
(2)当m=10,n=8时，中途上车的乘客有$\frac{13}{2}$×10-$\frac{9}{2}$×8=29(人).

10 已知一个多项式加上$x^{2}y - 3xy^{2}得2x^{2}y - xy^{2}$,求这个多项式.
佳琪的解答过程如下：
这个多项式为$2x^{2}y - xy^{2}-x^{2}y - 3xy^{2}= x^{2}y - 4xy^{2}$.
请你判断佳琪的解答过程是否正确,若不正确,请写出正确的解答过程.

答案： 【解】佳琪的解答过程不正确.正确的解答过程如下：
根据题意得这个多项式为(2x²y-xy²)-(x²y-3xy²)=2x²y-xy²-x²y+3xy²=x²y+2xy².