第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
13[2025安徽亳州期末]尺规作图(不写作法,保留作图痕迹):如图,已知平面上三点A,B,C.
(1)作射线AC,线段AB;
(2)作∠ABD= ∠BAC,交射线AC于点D.
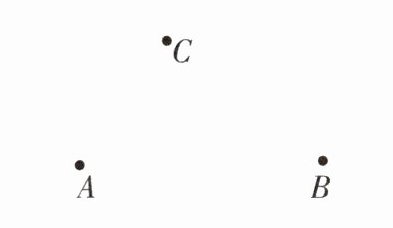
(1)作射线AC,线段AB;
(2)作∠ABD= ∠BAC,交射线AC于点D.

答案:
【解】
(1)如图所示,射线AC,线段AB即为所求.
(2)如图,∠ABD,点D即为所求.

【解】
(1)如图所示,射线AC,线段AB即为所求.
(2)如图,∠ABD,点D即为所求.

14 如图,已知点A,B,C,D,E在同一直线上,且AC= BD,E是线段BC的中点.
(1)判断点E是不是线段AD的中点,并说明理由.
(2)当AD= 10,AB= 3时,求线段BE的长度.
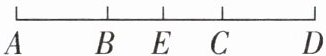
(1)判断点E是不是线段AD的中点,并说明理由.
(2)当AD= 10,AB= 3时,求线段BE的长度.
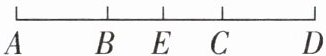
答案:
【解】
(1)点E是线段AD的中点. 理由:因为AC = BD,所以AB + BC = BC + CD,所以AB = CD. 因为点E是线段BC的中点,所以BE = EC,所以AB + BE = CD + EC,即AE = ED,所以点E是线段AD的中点.
(2)因为AD = 10,AB = CD = 3,所以BC = AD - 2AB = 10 - 2×3 = 4,所以BE = $\frac{1}{2}$BC = $\frac{1}{2}$×4 = 2.
(1)点E是线段AD的中点. 理由:因为AC = BD,所以AB + BC = BC + CD,所以AB = CD. 因为点E是线段BC的中点,所以BE = EC,所以AB + BE = CD + EC,即AE = ED,所以点E是线段AD的中点.
(2)因为AD = 10,AB = CD = 3,所以BC = AD - 2AB = 10 - 2×3 = 4,所以BE = $\frac{1}{2}$BC = $\frac{1}{2}$×4 = 2.
15[2025山东青岛期中]时钟是我们日常生活中常见的生活用品,钟表上的时针和分针都绕其轴心旋转,表盘中数字1~12均匀分布,分针转动一周(360°)需要60分,时针转动一周的$\frac{1}{12}$需要60分,这样,分针的转速为每分转6°,时针的转速为每分转$(\frac{1}{2})°.【$课题学习】
3:20时,时针与分针所成角为多少度?解决这个问题,可以先考虑三点整,时针与分针所成角为90°;从3:00到3:20,我们可以先计算分针转动的角度:20×6°= 120°,时针转动的角度:$20×(\frac{1}{2})°= 10°,$120°-(90°+10°)= 20°.故3:20时,时针与分针所成角是20°.
【问题解决】
(1)当3:30时,时针与分针所成角的度数是____.
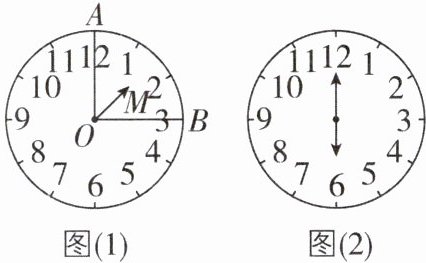
(2)如图(1),表盘上的点A对应数字“12”,点B对应数字“3”,若分针OM从OA的位置开始转动,经过多少分,OM第一次平分∠AOB?
(3)当时针和分针所成角为180°时,形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“美妙时刻”,如图(2),六点整就是一个“美妙时刻”,从0时到24时共有____个“美妙时刻”.
3:20时,时针与分针所成角为多少度?解决这个问题,可以先考虑三点整,时针与分针所成角为90°;从3:00到3:20,我们可以先计算分针转动的角度:20×6°= 120°,时针转动的角度:$20×(\frac{1}{2})°= 10°,$120°-(90°+10°)= 20°.故3:20时,时针与分针所成角是20°.
【问题解决】
(1)当3:30时,时针与分针所成角的度数是____.
(2)如图(1),表盘上的点A对应数字“12”,点B对应数字“3”,若分针OM从OA的位置开始转动,经过多少分,OM第一次平分∠AOB?
(3)当时针和分针所成角为180°时,形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“美妙时刻”,如图(2),六点整就是一个“美妙时刻”,从0时到24时共有____个“美妙时刻”.

答案:
【解】
(1)三点整,时针与分针所成角为90°,从3:00到3:30,分针转动的角度:30×6° = 180°,时针转动的角度:30×($\frac{1}{2}$)° = 15°,180° - (90° + 15°) =75°.故答案为75°.
(2)设经过t分,OM第一次平分∠AOB.因为OM平分∠AOB,所以∠AOM = $\frac{1}{2}$∠AOB,即6t = $\frac{1}{2}$×90,解得t = 7.5,故经过7.5分,OM第一次平分∠AOB.
(3)相邻两次成180°角之间,分针比时针多走360°,花费的时间为$\frac{360}{6 - \frac{1}{2}}$ = $\frac{720}{11}$(分),24时 = 1440分,1440÷$\frac{720}{11}$ = 22(个).故答案为22.
(1)三点整,时针与分针所成角为90°,从3:00到3:30,分针转动的角度:30×6° = 180°,时针转动的角度:30×($\frac{1}{2}$)° = 15°,180° - (90° + 15°) =75°.故答案为75°.
(2)设经过t分,OM第一次平分∠AOB.因为OM平分∠AOB,所以∠AOM = $\frac{1}{2}$∠AOB,即6t = $\frac{1}{2}$×90,解得t = 7.5,故经过7.5分,OM第一次平分∠AOB.
(3)相邻两次成180°角之间,分针比时针多走360°,花费的时间为$\frac{360}{6 - \frac{1}{2}}$ = $\frac{720}{11}$(分),24时 = 1440分,1440÷$\frac{720}{11}$ = 22(个).故答案为22.
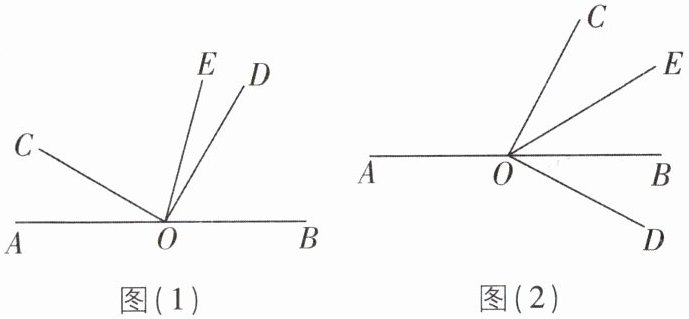
16 已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图(1),若∠AOC= 30°,求∠COE,∠DOB的度数.
(2)如图(1),若∠AOC= α,求∠DOE的度数(用含α的代数式表示).
(3)将图(1)中的∠COD绕顶点O顺时针旋转至图(2)的位置,探究∠AOC与∠DOE的数量关系,并说明理由.
(1)如图(1),若∠AOC= 30°,求∠COE,∠DOB的度数.
(2)如图(1),若∠AOC= α,求∠DOE的度数(用含α的代数式表示).
(3)将图(1)中的∠COD绕顶点O顺时针旋转至图(2)的位置,探究∠AOC与∠DOE的数量关系,并说明理由.

答案:
【解】
(1)因为∠AOC = 30°,∠COD是直角,所以∠BOC = 180° - ∠AOC = 150°,∠COD = 90°,所以∠BOD = 180° - ∠AOC - ∠COD = 60°.因为OE平分∠BOC,所以∠COE = $\frac{1}{2}$∠BOC = 75°.
(2)因为∠AOC = α,∠COD是直角,所以∠BOC = 180° - ∠AOC = 180° - α,∠COD = 90°,所以∠BOD = 180° - ∠AOC - ∠COD = 90° - α.因为OE平分∠BOC,所以∠BOE = $\frac{1}{2}$∠BOC = 90° - $\frac{1}{2}$α,所以∠DOE = ∠BOE - ∠BOD = 90° - $\frac{1}{2}$α - (90° - α) = $\frac{1}{2}$α.
(3)∠DOE = $\frac{1}{2}$∠AOC.理由如下:设∠AOC = β,因为∠COD是直角,所以∠BOC = 180° - ∠AOC = 180° - β,∠COD = 90°.因为OE平分∠BOC,所以∠COE = $\frac{1}{2}$∠BOC = 90° - $\frac{1}{2}$β,所以∠DOE = 90° - ∠COE = 90° - (90° - $\frac{1}{2}$β) = $\frac{1}{2}$β,即∠DOE = $\frac{1}{2}$∠AOC.
(1)因为∠AOC = 30°,∠COD是直角,所以∠BOC = 180° - ∠AOC = 150°,∠COD = 90°,所以∠BOD = 180° - ∠AOC - ∠COD = 60°.因为OE平分∠BOC,所以∠COE = $\frac{1}{2}$∠BOC = 75°.
(2)因为∠AOC = α,∠COD是直角,所以∠BOC = 180° - ∠AOC = 180° - α,∠COD = 90°,所以∠BOD = 180° - ∠AOC - ∠COD = 90° - α.因为OE平分∠BOC,所以∠BOE = $\frac{1}{2}$∠BOC = 90° - $\frac{1}{2}$α,所以∠DOE = ∠BOE - ∠BOD = 90° - $\frac{1}{2}$α - (90° - α) = $\frac{1}{2}$α.
(3)∠DOE = $\frac{1}{2}$∠AOC.理由如下:设∠AOC = β,因为∠COD是直角,所以∠BOC = 180° - ∠AOC = 180° - β,∠COD = 90°.因为OE平分∠BOC,所以∠COE = $\frac{1}{2}$∠BOC = 90° - $\frac{1}{2}$β,所以∠DOE = 90° - ∠COE = 90° - (90° - $\frac{1}{2}$β) = $\frac{1}{2}$β,即∠DOE = $\frac{1}{2}$∠AOC.
查看更多完整答案,请扫码查看


