《2025年初中必刷题七年级数学上册北师大版》

1 [2024宁夏银川质检,中]已知线段AB,画出它的中点C,再画出BC的中点D,再画出AD的中点E,再画出AE的中点F,那么AF等于AB的( )

A.$ \frac{1}{4} $
B.$ \frac{3}{8} $
C.$ \frac{1}{8} $
D.$ \frac{3}{16} $

答案： D 【解析】根据题意作图如下:结合图形和题意可知$AF = \frac{1}{2}AE = \frac{1}{4}AD$，$BD = \frac{1}{2}BC = \frac{1}{4}AB$。因为$AD = AB - BD = AB - \frac{1}{4}AB = \frac{3}{4}AB$，所以$AF = \frac{1}{4}AD = \frac{1}{4}×\frac{3}{4}AB = \frac{3}{16}AB$，故选 D。

2 新考向数学文化[较难]康托尔用以下方法构造的在一条线段上的一些点的集合,称为康托尔集。如图,取一条长度为1的线段,将它三等分,去掉中间一段,剩下两段,这称为第一阶段；将剩下的两段再分别三等分,各去掉中间一段,剩下更短的四段,这称为第二阶段；…,将这样的操作无限地重复下去,剩下的无数个点就称为康托尔集。那么经过第四个阶段后,剩下的线段的长度之和为( )


A.$ \frac{4}{27} $
B.$ \frac{16}{81} $
C.$ \frac{8}{243} $
D.$ \frac{16}{243} $

答案： B 【解析】根据题意知，经过第一阶段后，剩下的线段的长度之和为$\frac{2}{3}$，经过第二阶段后，剩下的线段的长度之和为$\frac{2}{3}×\frac{2}{3}=(\frac{2}{3})^{2}$，经过第三阶段后，剩下的线段的长度之和为$\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=(\frac{2}{3})^{3}$，则经过第四阶段后，剩下的线段的长度之和为$\frac{2}{3}×\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=(\frac{2}{3})^{4}=\frac{16}{81}$，故选 B。

3 [2025北京通州区期末,中]延长线段AB到C,使$ BC = \frac{1}{3}AB $,反向延长线段AB到D,使$ AD = \frac{1}{2}AC $,点E为AB的中点,点F为CD的中点。若$ AB = 12cm $,则线段EF的长为______cm。

答案： 2 【解析】根据题意，令$BC = xcm$，则$AB = 3xcm$，所以$AC = x + 3x = 4x(cm)$，则$AD = \frac{1}{2}AC = \frac{1}{2}·4x = 2x(cm)$，$CD = 4x + 2x = 6x(cm)$。如图所示，因为$AB = 12cm$，所以$3x = 12$，解得$x = 4$，所以$CD = 24cm$，$AD = 8cm$。因为点 E 为 AB 的中点，点 F 为 CD 的中点，所以$AE = 6cm$，$DF = 12cm$，所以$AF = DF - AD = 12 - 8 = 4(cm)$，所以$EF = AE - AF = 6 - 4 = 2(cm)$。故答案为 2。

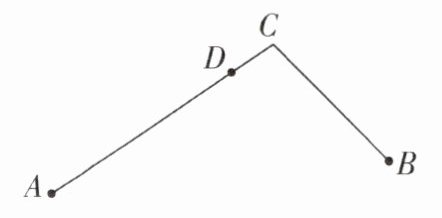
4 [较难]如图,有公共端点C的两条线段AC,BC组成一条折线A-C-B,若该折线A-C-B上一点D把这条折线分成相等的两部分,我们把这个点D叫作这条折线的“折中点”。
(1)若$ AC = BC $,则点D与点______重合；
(2)若E为线段AC的中点,$ EC = 5cm $,$ CD = 2cm $,则BC的长为______。

答案：
(1)C
(2)6 cm 或 14 cm 【解析】
(1)当$AC = BC$时，点 D 与点 C 重合。
(2)①当点 D 在线段 AC 上时，因为 E 为线段 AC 的中点，$EC = 5cm$，所以$AC = 2CE = 10cm$。因为$CD = 2cm$，所以$AD = AC - CD = 8cm$。因为$BC + CD = AD = 8cm$，所以$BC = 8 - 2 = 6(cm)$。②当点 D 在线段 BC 上时，因为 E 为线段 AC 的中点，$EC = 5cm$，所以$AC = 2CE = 10cm$。因为$CD = 2cm$，所以$AC + CD = 12cm$。因为$BD = AC + CD = 12cm$，所以$BC = 12 + 2 = 14(cm)$。综上，BC 的长为 6 cm 或 14 cm。

5 [较难]如图,M是定长线段AB上一定点,C,D两点分别从M,B出发,以$ 1cm/s $,$ 3cm/s $的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)。
(1)若$ AB = 10cm $,当点C,D运动了2s时,求$ AC + MD $的值。
(2)若点C,D运动时,总有$ MD = 3AC $,直接填空：$ AM = $______AB。
(3)在(2)的条件下,N是直线AB上一点,且$ AN - BN = MN $,求$ \frac{MN}{AB} $的值。

答案：

(1)当点 C，D 运动了 2 s 时，$CM = 2cm$，$BD = 6cm$。又因为$AB = 10cm$，所以$AC + MD = AB - CM - BD = 10 - 2 - 6 = 2(cm)$。
(2)$\frac{1}{4}$ 【解析】设运动时间为 t s，则$CM = tcm$，$BD = 3tcm$。因为$AC = AM - t$，$MD = BM - 3t$，$MD = 3AC$，所以$BM - 3t = 3(AM - t)$，即$BM = 3AM$。因为$BM = AB - AM$，所以$AB - AM = 3AM$，所以$AM = \frac{1}{4}AB$。故答案为$\frac{1}{4}$。
(3)①当点 N 在线段 AB 上时，如图
(1)。A←NB 图
(1)因为$AN - BN = MN$，$AN - AM = MN$，所以$BN = AM = \frac{1}{4}AB$，所以$MN = \frac{1}{2}AB$，即$\frac{MN}{AB} = \frac{1}{2}$。②当点 N 在线段 AB 的延长线上时，如图
(2)。 因为$AN - BN = MN$，$AN - BN = AB$，所以$MN = AB$，即$\frac{MN}{AB} = 1$。综上所述，$\frac{MN}{AB}$的值为$\frac{1}{2}$或 1。

6 思想方法分类讨论[较难]点C在线段AB上,若$ BC = 2AC 或 AC = 2BC $,则称点C是线段AB的“雅点”,线段AC,BC互为“雅点”伴侣线段。
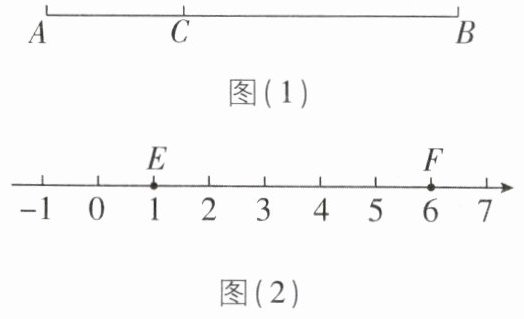
(1)如图(1),若点C为线段AB的“雅点”,$ AC = 6(AC ＜ BC) $,则$ AB = $______；
(2)如图(2),数轴上有一点E表示的数为1,向右平移5个单位到达点F。若点G在射线EF上,且线段GF与以E,F,G中某两个点为端点的线段互为“雅点”伴侣线段,请写出点G所表示的数。(写出必要的推理步骤)

答案：

(1)18 【解析】因为点 C 为线段 AB 的“雅点”，$AC = 6(AC ＜ BC)$，所以$BC = 2AC = 12$，所以$AB = AC + BC = 18$。故答案为 18。
(2)因为点 G 在射线 EF 上，且线段 GF 与以 E，F，G 中某两个点为端点的线段互为“雅点”伴侣线段，所以分以下四种情况：①当 G 在线段 EF 上且$EG = 2FG$时，如图
(1)。 因为$EG = 2FG$，$EG + FG = 5$，所以$EG = \frac{10}{3}$。因为 E 表示的数为 1，所以 G 表示的数为$1 + \frac{10}{3} = \frac{13}{3}$。②当 G 在线段 EF 上且$FG = 2EG$时，如图
(2)。 因为$FG = 2EG$，$EG + FG = 5$，所以$EG = \frac{5}{3}$。因为 E 表示的数为 1，所以 G 表示的数为$1 + \frac{5}{3} = \frac{8}{3}$。③当 G 在线段 EF 的延长线上且$EF = 2FG$时，如图
(3)。 因为$EF = 2FG$，$EF = 5$，所以$FG = 2.5$，所以 G 表示的数为$1 + 5 + 2.5 = 8.5$。④当 G 在线段 EF 的延长线上且$FG = 2EF$时，如图
(4)。 因为$FG = 2EF$，$EF = 5$，所以$FG = 10$，所以 G 表示的数为$1 + 5 + 10 = 16$。综上所述，点 G 所表示的数为$\frac{13}{3}$或$\frac{8}{3}$或 8.5 或 16。