《2025年初中必刷题七年级数学上册北师大版》

1 [2025 河北石家庄期中,中]把直角三角板的直角顶点C放在直尺的一边MN上.
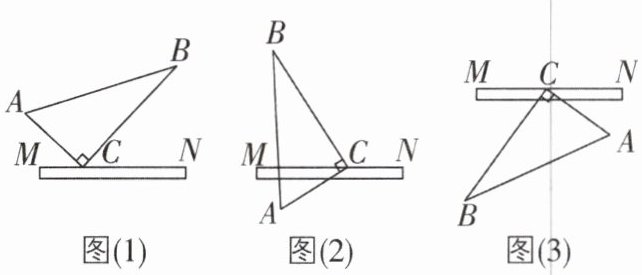
(1)点A和点B在直线MN的上方(如图(1)),此时$∠ACM与∠BCN的数量关系是∠ACM + ∠BCN = $____;
(2)当把这把直角三角板绕顶点C旋转到点A在直线MN的下方、点B仍然在直线MN的上方时(如图(2)),$∠ACM与∠BCN$的数量关系是____;
(3)当把这把直角三角板绕顶点C旋转到点A和点B都在直线MN的下方时(如图(3)),$∠ACM与∠BCN$的数量关系是____.

答案： 1.
(1)90°
(2)∠BCN-∠ACM=90°
(3)∠ACM+∠BCN=270°【解析】
(1)∠ACM+∠BCN=180°-∠ACB=180°-90°=90°.故答案为90°.
(2)因为∠BCN=180°-∠BCM,∠ACM=90°-∠BCM,所以∠BCN-∠ACM=(180°-∠BCM)-(90°-∠BCM)=90°.故答案为∠BCN-∠ACM=90°.
(3)因为∠BCN=180°-∠BCM,∠ACM=90°+∠BCM,所以∠BCN+∠ACM=(180°-∠BCM)+(90°+∠BCM)=270°.故答案为∠ACM+∠BCN=270°.

2 [2025 广东潮州期末,中]如图(1),O为直线AB上一点,过点O作射线OC,$∠AOC = 30^{\circ}$,将一直角三角板($∠M = 30^{\circ}$)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与射线OC都在直线AB的上方.(注:本题中最大旋转角度为$180^{\circ}$)
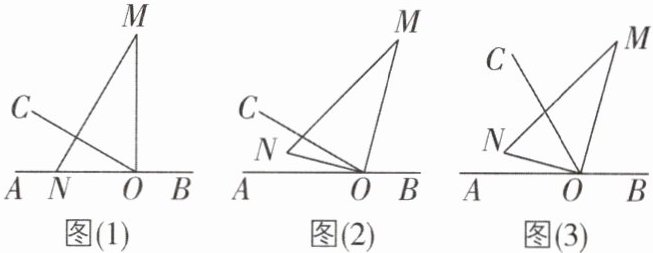
(1)将图(1)中的三角板绕点O以每秒$3^{\circ}$的速度沿顺时针方向旋转.如图(2),经过t秒后,$∠AON = $____度(用含t的式子表示),若OM恰好平分$∠BOC$,则$t = $____.
(2)在(1)的基础上,若三角板在转动的同时,射线OC也绕O点以每秒$6^{\circ}$的速度沿顺时针方向旋转,如图(3),经过t秒后,$∠AOC = $____度(用含t的式子表示),若OC平分$∠MON$,求t的值.

答案： 2.【解】
(1)由题可知∠AON=(3t)°.因为∠AOC=30°,所以∠BOC=150°.因为OM平分∠BOC,∠MON=90°,所以∠COM= $\frac{1}{2}$∠BOC=75°,所以∠CON=∠MON-∠MOC=15°,所以∠AON=∠AOC-∠CON=30°-15°=15°,所以t=15°÷3°=5.故答案为(3t),5.
(2)由题可知∠AOC=(30+6t)°.因为∠MON=90°,OC平分∠MON,所以∠CON=∠COM=45°,所以∠AOC-∠AON=∠CON=45°,所以30+6t-3t=45,解得t=5.故答案为(30+6t).

3 [2024 四川南充期末,中]已知$∠AOB = 80^{\circ}$,$∠COD = 50^{\circ}$,OE平分$∠AOC$,OF平分$∠BOD$.
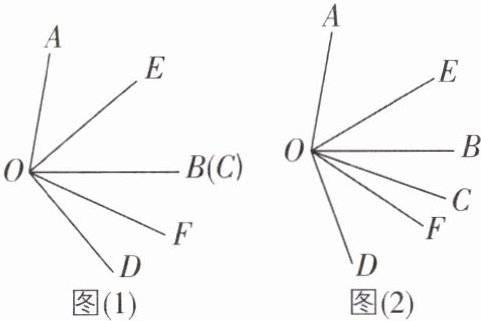
(1)如图(1),当OB,OC重合时,求$∠EOF$的度数.
(2)将图(1)中$∠COD$绕点O顺时针旋转$n^{\circ}$($0 ＜ n ＜ 50$)得到图(2),$∠EOF$的度数是否为定值?若是定值,求出$∠EOF$的度数;若不是,请说明理由.
(3)在(2)的条件下,若满足$∠AOD - ∠EOF = \frac{3}{2}(∠BOE + ∠COF)$,求n的值.

答案： 3.【解】
(1)因为OB与OC重合,OE平分∠AOC,所以∠EOB= $\frac{1}{2}$∠AOB=40°.因为OF平分∠BOD,所以∠BOF= $\frac{1}{2}$∠COD=25°,所以∠EOF=∠EOB+∠BOF=65°.
(2)∠EOF的度数是定值.由旋转可知∠BOC=n°,所以∠AOC=80°+n°,∠BOD=50°+n°.因为OE平分∠AOC,所以∠COE= $\frac{1}{2}$∠AOC.因为OF平分∠BOD,所以∠BOF= $\frac{1}{2}$∠BOD,所以∠EOF=∠COE+∠COF=∠COE+∠BOF-∠BOC= $\frac{1}{2}$×(80°+n°)+ $\frac{1}{2}$×(50°+n°)-n°=65°,所以∠EOF的度数是定值,为65°.
(3)因为∠AOB=80°,∠COD=50°,∠BOC=n°,所以∠AOD=∠AOB+∠COD+∠BOC=80°+50°+n°=130°+n°.因为∠AOD-∠EOF= $\frac{3}{2}$(∠BOE+∠COF)= $\frac{3}{2}$(∠EOF-∠BOC),且∠EOF=65°,所以130°+n°-65°= $\frac{3}{2}$(65°-n°),解得n=13,所以n的值为13.