《2025年初中必刷题七年级数学上册北师大版》

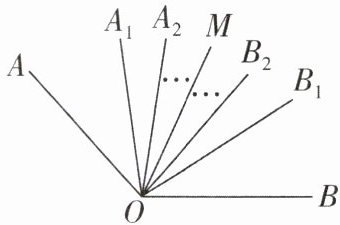
1[2024河北唐山期中,中]如图,$∠AOB= α,$$OA_{1},OB_{1}分别是∠AOM和∠MOB$的平分线,$OA_{2},OB_{2}分别是∠A_{1}OM和∠MOB_{1}$的平分线,$OA_{3},OB_{3}分别是∠A_{2}OM和∠MOB_{2}$的平分线,…,$OA_{n},OB_{n}分别是∠A_{n-1}OM和∠MOB_{n-1}$的平分线,则$∠A_{n}OB_{n}$的度数是 ( )


A.$\frac {α}{n}$
B.$\frac {α}{2^{n-1}}$
C.$\frac {α}{2^{n}}$
D.$\frac {α}{n^{2}}$

答案： C 【解析】因为∠AOB=α，OA₁,OB₁分别是∠AOM和∠MOB的平分线，所以∠A₁OM=$\frac{1}{2}$∠AOM，∠B₁OM=$\frac{1}{2}$∠BOM，所以∠A₁OB₁=$\frac{1}{2}$(∠AOM + ∠BOM)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$α；因为OA₂,OB₂分别是∠A₁OM和∠MOB₁的平分线，所以∠A₂OM=$\frac{1}{2}$∠A₁OM，∠B₂OM=$\frac{1}{2}$∠B₁OM，所以∠A₂OB₂=$\frac{1}{2}$(∠A₁OM + ∠B₁OM)=$\frac{1}{2}$∠A₁OB₁=$\frac{1}{2}$×$\frac{1}{2}$∠AOB=$\frac{α}{2^{2}}$；因为OA₃,OB₃分别是∠A₂OM和∠MOB₂的平分线，所以∠A₃OM=$\frac{1}{2}$∠A₂OM，∠B₃OM=$\frac{1}{2}$∠B₂OM，所以∠A₃OB₃=$\frac{1}{2}$(∠A₂OM + ∠B₂OM)=$\frac{1}{2}$∠A₂OB₂=$\frac{1}{2}$×$\frac{1}{2}$∠A₁OB₁=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$∠AOB=$\frac{α}{2^{3}}$；…，由此规律得∠AₙOBₙ=$\frac{α}{2^{n}}$，故选C。

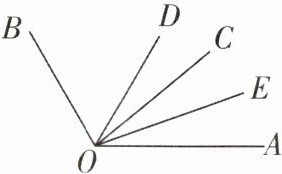
2[2024江苏无锡期末,中](1)如图,若$∠AOB= $$120^{\circ },∠AOC= 40^{\circ }$,OD,OE分别平分$∠AOB,$$∠AOC$,求$∠DOE$的度数;
(2)若$∠AOB,∠AOC$是平面内两个角,$∠AOB= $$m^{\circ },∠AOC= n^{\circ }(0\lt n\lt m\lt 180)$,OD,OE分别平分$∠AOB,∠AOC$,求$∠DOE$的度数.(用含m,n的代数式表示)

答案：

(1)因为∠AOB = 120°，OD平分∠AOB，所以∠AOD = ∠BOD = $\frac{1}{2}$∠AOB = 60°。因为OE平分∠AOC，∠AOC = 40°，所以∠AOE = $\frac{1}{2}$∠AOC = 20°，所以∠DOE = ∠AOD - ∠AOE = 60° - 20° = 40°。
(2)若射线OC在∠AOB的内部，如图
(1)。因为∠AOB = m°，∠AOC = n°，OD,OE分别平分∠AOB,∠AOC，所以∠DOE = ∠AOD - ∠AOE = $\frac{1}{2}$∠AOB - $\frac{1}{2}$∠AOC = $\frac{1}{2}$(m - n)°，所以当射线OC在∠AOB的内部时，∠DOE = $\frac{1}{2}$(m - n)°。

若射线OC在∠AOB外部，如图
(2)。因为∠AOB = m°，∠AOC = n°，OD,OE分别平分∠AOB,∠AOC，所以∠DOE = ∠AOD + ∠AOE = $\frac{1}{2}$∠AOB + $\frac{1}{2}$∠AOC = $\frac{1}{2}$(n + m)°，所以当射线OC在∠AOB的外部时，∠DOE = $\frac{1}{2}$(n + m)°。

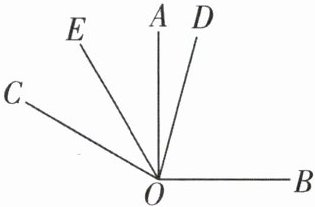
3[2024内蒙古包头东河区期末,中]如图,已知在同一平面内,$∠AOB= 90^{\circ },∠AOC= 60^{\circ }.$
(1)填空:$∠BOC= $____;
(2)如果OD平分$∠BOC$,OE平分$∠AOC$,求$∠DOE$的度数;
(3)如果在(2)的条件下将$∠AOC= 60^{\circ }改为∠AOC= 2α(0^{\circ }＜α＜45^{\circ })$,其他条件不变,求$∠DOE$的度数.

答案：
(1)150°
(2)由
(1)知∠BOC = 150°。因为OD平分∠BOC，所以∠DOC = $\frac{1}{2}$∠BOC = 75°。因为OE平分∠AOC，∠AOC = 60°，所以∠COE = $\frac{1}{2}$∠AOC = 30°，所以∠DOE = ∠DOC - ∠COE = 45°。
(3)因为∠AOB = 90°，∠AOC = 2α，所以∠BOC = ∠AOB + ∠AOC = 90° + 2α。因为OD平分∠BOC，所以∠DOC = $\frac{1}{2}$∠BOC = 45° + α。因为OE平分∠AOC，所以∠COE = $\frac{1}{2}$∠AOC = α，所以∠DOE = ∠DOC - ∠COE = 45°。

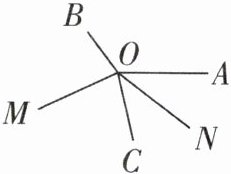
4[2024陕西西安碑林区校级期末,中]如图,$∠AOB= 126^{\circ }$,射线OC在$∠AOB$外,且$∠BOC= 2∠AOC$,若OM平分$∠BOC$,ON平分$∠AOC$,则$∠MON= $____.

答案： 117° 【解析】因为∠AOB + ∠BOC + ∠AOC = 360°，所以∠BOC + ∠AOC = 360° - ∠AOB。因为OM平分∠BOC，ON平分∠AOC，所以∠MOC = $\frac{1}{2}$∠BOC，∠CON = $\frac{1}{2}$∠AOC，所以∠MON = ∠MOC + ∠CON = $\frac{1}{2}$∠BOC + $\frac{1}{2}$∠AOC = $\frac{1}{2}$(∠BOC + ∠AOC) = $\frac{1}{2}$(360° - ∠AOB) = 180° - $\frac{1}{2}$∠AOB = 180° - $\frac{1}{2}$×126° = 117°，故答案为117°。