第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1[2025吉林长春质检]如图是几何体的展开图,这个几何体是( )

A.圆柱
B.圆锥
C.四棱柱
D.三棱柱

A.圆柱
B.圆锥
C.四棱柱
D.三棱柱
答案:
D 【解析】因为展开图由三个长方形和两个三角形组成,所以这个几何体是三棱柱,故选D.
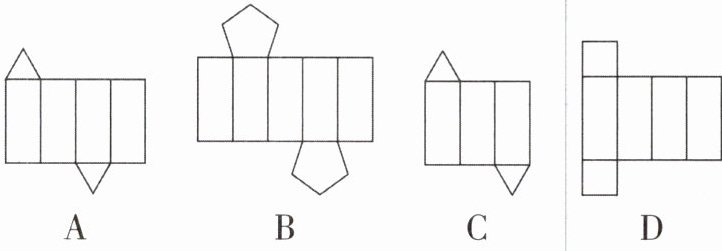
2[2025江苏盐城质检]下列图形经过折叠不能围成棱柱的是( )

答案:
A 【解析】A不能围成棱柱,B可以围成五棱柱,C可以围成三棱柱,D可以围成四棱柱,故选A.
3[2024山东威海文登区期中]一个棱柱共有12个顶点,设这个棱柱共有m个面,共有n条棱,将它展开成一个平面图形需要剪开p条棱,则m+n-p=______。
答案:
15 【解析】因为这个棱柱共有12个顶点,所以它是六棱柱,所以 m = 6 + 2 = 8,n = 3×6 = 18,p = 11,所以 m + n - p = 8 + 18 - 11 = 15. 故答案为15.
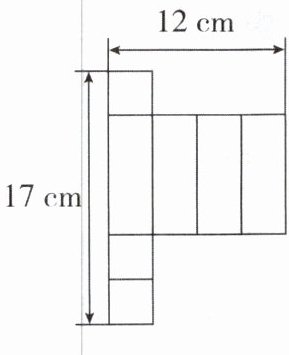
4[2024江苏泰州姜堰区期末]在学习棱柱的展开与折叠时,老师让同学们用若干个正方形和长方形拼成一个长方体的展开图。拼完后(如图),小明觉得所拼图形似乎存在问题。
(1)请你帮小明分析一下所拼图形是否存在问题,若有多余块,请把图中多余块涂上阴影;若还缺少,请直接在原图中补全。
(2)长方体共有______条棱,若将一个长方体沿某些棱剪开展成(1)中修正后的平面图形,需要剪开______条棱。
(3)根据图中的数据,求出修正后的展开图所折叠而成的长方体的体积。
(1)请你帮小明分析一下所拼图形是否存在问题,若有多余块,请把图中多余块涂上阴影;若还缺少,请直接在原图中补全。
(2)长方体共有______条棱,若将一个长方体沿某些棱剪开展成(1)中修正后的平面图形,需要剪开______条棱。
(3)根据图中的数据,求出修正后的展开图所折叠而成的长方体的体积。

答案:
【解】
(1)有多余块,如图所示.
(2)长方体共有12条棱,若将一个长方体沿某些棱剪开展成
(1)中修正后的平面图形,需要剪开7条棱,故答案为12,7.
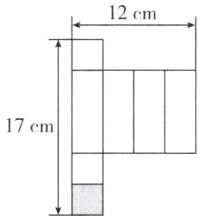
(3)底面正方形边长为 12÷4 = 3(cm),长方体的高为 17 - 3×3 = 8(cm),所以长方体体积为 3×3×8 = 72($cm^3$).
答:修正后的展开图所折叠而成的长方体的体积为 72 $cm^3$.
【解】
(1)有多余块,如图所示.
(2)长方体共有12条棱,若将一个长方体沿某些棱剪开展成
(1)中修正后的平面图形,需要剪开7条棱,故答案为12,7.

(3)底面正方形边长为 12÷4 = 3(cm),长方体的高为 17 - 3×3 = 8(cm),所以长方体体积为 3×3×8 = 72($cm^3$).
答:修正后的展开图所折叠而成的长方体的体积为 72 $cm^3$.
5[2025黑龙江哈尔滨期末]小红想设计制作一个有盖的圆柱形礼品盒,下列展开图中设计正确的是( )


答案:
C 【解析】A能折出三棱柱,B能折出无盖圆柱,C能折出圆柱,D能折出长方体,故选C.
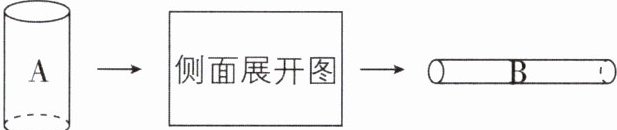
6[2024四川成都期中]如图,用高为6cm、底面直径为4cm的圆柱A的侧面展开图,围成不同于圆柱A的另一个圆柱B,则圆柱B的体积为______cm³。

答案:
36 【解析】根据题意,得到圆柱B的底面周长是6 cm,高是4π cm,则圆柱B的体积为$\pi(\frac{6}{2\pi})^2×4\pi = 36$($cm^3$). 故答案为36.
7[2025广东广州期末]如图,S是圆锥的顶点,AB是圆锥底面的直径,M是SA的中点。在圆锥的侧面上过点B,M嵌有一圈路径最短的金属丝,现将圆锥侧面沿SA剪开,所得圆锥的侧面展开图可能是( )
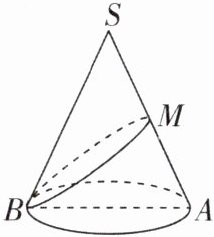



答案:
B 【解析】因为圆锥侧面展开图是扇形,M是SA的中点,在圆锥的侧面上过点B,M嵌有一圈路径最短的金属丝,所以现将圆锥侧面沿SA剪开,所得圆锥的侧面展开图可能是B,故选B.
8[2024宁夏银川期中](1)请写出下列展开图对应的几何体的名称:①______;②______;③______。
(2)③中的侧面展开图的宽(较短边)为8cm,圆的半径为2cm,其所对应的几何体的表面积为______。(结果保留π)

(2)③中的侧面展开图的宽(较短边)为8cm,圆的半径为2cm,其所对应的几何体的表面积为______。(结果保留π)

答案:
(1)①圆锥 ②三棱锥 ③圆柱
(2)40π $cm^2$
【解析】
(2)圆柱的表面积为$2×\pi×2^2 + 2×\pi×2×8 = 40\pi$($cm^2$),故答案为 40π $cm^2$.
(1)①圆锥 ②三棱锥 ③圆柱
(2)40π $cm^2$
【解析】
(2)圆柱的表面积为$2×\pi×2^2 + 2×\pi×2×8 = 40\pi$($cm^2$),故答案为 40π $cm^2$.
查看更多完整答案,请扫码查看


