《2025年初中必刷题七年级数学上册北师大版》

1 [2025 湖北随州质检]如图,填在各方格中的三个数之间均具有相同的规律,根据此规律,$n$的值是( )


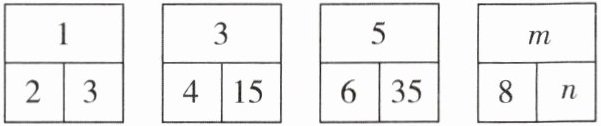
A.48
B.56
C.63
D.74

答案： C 【解析】从方格上方的数1,3,5可以推出m=7,第一个方格中:3=1×2+1,第二个方格中:15=3×4+3,第三个方格中:35=5×6+5,所以第四个方格中:n=7×8+7=63.

2 如图是某月的日历表,用带阴影的方框恰好盖住四个数,若这样的阴影方框可以上下左右移动,覆盖了这张日历表中的4个数,设$a表示的数是x$,则这4个数的和为____.(用含$x$的代数式表示)

答案： 4x+14 【解析】由题意得b表示的数是x+1,c表示的数是x+6,d表示的数是x+7,所以这4个数的和为x+x+1+x+6+x+7=4x+14.故答案为4x+14.

3 [2025 河南开封期末]在日历上,我们可以发现其中某些数满足一定的规律.如图是2025年1月份的日历,任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如:$8×14 - 7×15 = 7$,$24×30 - 23×31 = 7$,发现结果都是7.若将方框部分左上角的数字设为$n$($n$为正整数),用含有$n$的等式表示这一规律为____.

答案： (n+1)(n+7)-n(n+8)=7 【解析】日历中所示的方框左上角数字为n,则其余三个数从小到大依次是n+1,n+7,n+8,所以用含有n的等式表示这一规律为(n+1)(n+7)-n(n+8)=7.故答案为(n+1)(n+7)-n(n+8)=7.

4 [2024 黑龙江牡丹江中考]如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形,第2个图有7个三角形,第3个图有10个三角形,…,按照此规律排列下去,第674个图中三角形的个数是( )


A.2022
B.2023
C.2024
D.2025

答案： B 思路分析 探索图形中的规律直接观察发现相邻图形的关系用代数式表示规律并验证计算与图形相关的数据找出数据间的变化规律探索数据与序号的关系 【解析】题中第1个图有4个三角形,即4=3×1+1,第2个图有7个三角形，即7=3×2+1,第3个图有10个三角形，即10=3×3+1,...,按此规律排列下去，第n个图有(3n+1)个三角形，则第674个图中三角形的个数为3×674+1=2023.故选B.

5 [2025 山东威海质检]如图,下列图形由多个完全相同的●组成,第一个图形有5个●,第二个图形有11个●,第三个图形有19个●,…,以此类推,第11个图形中●的个数为( )


A.131
B.132
C.155
D.156

答案： C 【解析】第一个图形有5=[(1+1)²+1]个•,第二个图形有11=[(2+1)²+2]个•,第三个图形有19=[(3+1)²+3]个•,...,发现规律:第n个图形有[(n+1)²+n]个•,所以第11个图形中•的个数为(11+1)²+11=155.故选C.

6 由白色小正方形和灰色小正方形组成的图形如图所示.

(1)第4个图形中白色小正方形和灰色小正方形的个数总和等于____.
(2)求第$n$个图形中白色小正方形和灰色小正方形的个数总和(用含$n$的代数式表示).

答案：
(1)32
(2)由题图得第1个图形中白色小正方形的个数为1²=1,灰色小正方形的个数为4×1=4,则其个数总和为1+4=5;第2个图形中白色小正方形的个数为2²=4,灰色小正方形的个数为4×2=8,则其个数总和为4+8=12;第3个图形中白色小正方形的个数为3²=9,灰色小正方形的个数为4×3=12,则其个数总和为9+12=21;...,则第n个图形中白色小正方形的个数为n²,灰色小正方形的个数为4n,则其个数总和为n²+4n.