《2025年初中必刷题七年级数学上册北师大版》

1 [2025云南昆明校级期中,中] 已知$a = -3$,$|a| = |b|$,则b的值为( )

A.+3
B.-3
C.0
D.±3

答案： D 【解析】因为$a=-3$,所以$|a|=3$. 因为$|a|=|b|$,所以$|b|=3$,所以$b=\pm 3$. 故选 D.

2 [2025甘肃陇南期末,中] 如图是一个正方体的展开图,若在其中的三个正方形A,B,C内分别填入适当的数,使折成正方体后相对面上的两个数恰好都互为相反数,则A,B,C内的数依次为( )


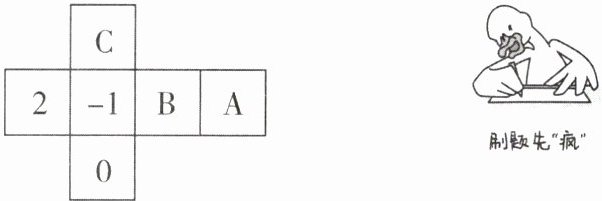
A.1,-2,0
B.-2,0,1
C.0,-2,1
D.-2,1,0

答案： A 【解析】由正方体的表面展开图可得,"A"与"-1"是相对面,"B"与"2"是相对面,"C"与"0"是相对面. 因为相对的面上的两个数互为相反数,所以 A,B,C 内的数依次为 1,-2,0. 故选 A.

3 [中] 定义：$a \vee b$表示a,b两数中较大的一个,$a \wedge b$表示a,b两数中较小的一个,则$[(-50) \vee (-52)] \vee [(-49) \wedge 51]$的结果是( )

A.-50
B.-52
C.-49
D.51

答案： C 【解析】根据题中的新定义得$[(-50)∨(-52)]∨[(-49)∧51]=(-50)∨(-49)=-49$. 故选 C.

4 [中] 在$-\frac{2}{3}的绝对值与-\frac{3}{2}$的相反数之间的整数是____.

答案： 1 【解析】因为$|-\frac{2}{3}|=\frac{2}{3}$,$-(-\frac{3}{2})=\frac{3}{2}$,所以$\frac{2}{3}$与$\frac{3}{2}$之间的整数为 1,故答案为 1.

5 [较难] 在-1.0426中用数字3替换其中的一个非零数字后,使所得的数最大,则被替换的数字是____.

答案： 4 【解析】被替换后所得的数可以是-3.0426,-1.0326,-1.0436,-1.0423. 因为$|-1.0326|＜|-1.0423|＜|-1.0436|＜|-3.0426|$,所以$-1.0326＞-1.0423＞-1.0436＞-3.0426$,所以最大的数是-1.0326,即被替换的数字是 4,故答案为 4.

6 [2025福建福州期中,中] 阅读材料,解答下列问题：
当$a ＞ 0$时,如$a = 6$,$|a| = |6| = 6$,故此时a的绝对值是它本身；
当$a = 0$时,$|a| = 0$,故此时a的绝对值是0；
当$a ＜ 0$时,如$a = -6$,$|a| = |-6| = 6 = -(-6)$,故此时a的绝对值是它的相反数,
所以一个数的绝对值要分三种情况,即$|a| = \begin{cases} a(a ＞ 0), \\ 0(a = 0), \\ -a(a ＜ 0). \end{cases} $
这种分析方法渗透了数学的分类讨论思想.
(1) 比较大小：$|-7|$____7,$|3|$____-3；(填“＞”“＜”或“=”)
(2) 请仿照材料中的分类讨论的方法,分析$|a|与-a$的大小关系.

答案： 【解】
(1)$|-7|=7$,$|3|＞-3$. 故答案为=,＞.
(2)当$a＞0$时,$|a|=a＞-a$;当$a=0$时,$|a|=0=-a$;当$a＜0$时,$|a|=-a$.

7 [中] (1) 当x取何值时,$|x - 2024|$有最小值？这个最小值是多少？
(2) 当x取何值时,$2024 - |x - 1|$有最大值？这个最大值是多少？

答案： 【解】
(1)因为$|x-2024|$是非负数,且非负数中最小的数是 0,所以当$x=2024$时,$|x-2024|$有最小值,这个最小值是 0.
(2)当$x=1$时,$|x-1|$有最小值,这个最小值为 0,此时$2024-|x-1|$有最大值,这个最大值是 2024.

8 [中] 已知零件的标准直径是100mm,超过标准直径长度的数量(mm)记作正数,不足标准直径长度的数量(mm)记作负数,检验员某次抽查了5件样品,检查结果如下：
|序号|1|2|3|4|5|
|直径长度/mm|+0.1|-0.15|+0.2|-0.05|+0.25|
(1) 指出哪件样品的直径最接近标准；
(2) 如果规定误差的绝对值在0.18mm之内是正品,误差的绝对值在0.18~0.22mm之间是次品,误差的绝对值超过0.22mm是废品,那么这5件样品分别属于哪类产品？

答案： 【解】
(1)第 4 件样品的直径最接近标准.
(2)因为$|+0.1|=0.1＜0.18$,$|-0.15|=0.15＜0.18$,$|-0.05|=0.05＜0.18$,所以第 1,2,4 件样品为正品;因为$|+0.2|=0.2$,$0.18＜0.2＜0.22$,所以第 3 件样品为次品;因为$|+0.25|=0.25＞0.22$,所以第 5 件样品为废品.