《2025年假日数学吉林出版集团股份有限公司八年级数学华师大版》

19. 【教材呈现】下面是《义务教育教科书数学八年级下册》(华师版)中第121页的部分内容.
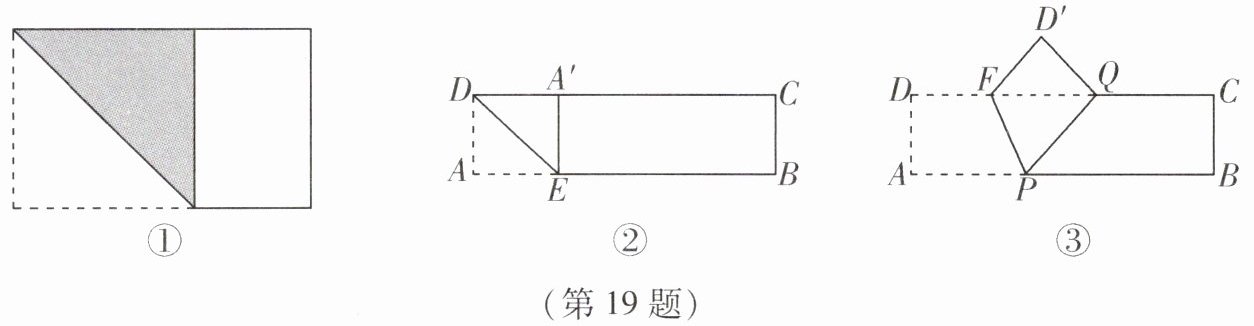
把一张矩形纸片如图①那样折一下,就可以裁出正方形纸片,为什么？
【问题解决】如图②,已知矩形纸片ABCD(AB＞AD),将矩形纸片沿过点D的直线折叠,使点A落在边DC上,点A的对应点为A',折痕为DE,点E在AB上. 求证：四边形AEA'D是正方形.
【规律探索】由“问题解决”可知,图②中的△A'DE为等腰三角形. 现将图②中的点A'沿DC向右平移至点Q处(点Q在点C的左侧),如图③,折痕为PF,点F在DC上,点P在AB上,那么△PQF还是等腰三角形吗？请说明理由.

答案： 【问题解决】$ \because $ 四边形 $ ABCD $ 是矩形，$ \therefore \angle A = \angle ADA' = 90^{\circ} $。
由翻折可知，$ \angle DA'E = \angle A = 90^{\circ} $，
$ \therefore \angle A = \angle ADA' = \angle DA'E = 90^{\circ} $，
$ \therefore $ 四边形 $ AEA'D $ 是矩形。
$ \because DA = DA' $，
$ \therefore $ 四边形 $ AEA'D $ 是正方形。
【规律探索】$ \triangle PQF $ 是等腰三角形。
理由：$ \because $ 四边形 $ ABCD $ 是矩形，
$ \therefore AB // CD $。$ \therefore \angle QFP = \angle APF $。
由翻折可知，$ \angle APF = \angle FPQ $，
$ \therefore \angle QFP = \angle FPQ $。$ \therefore QF = QP $。
$ \therefore \triangle PFQ $ 是等腰三角形。