《2025年假日数学吉林出版集团股份有限公司八年级数学华师大版》

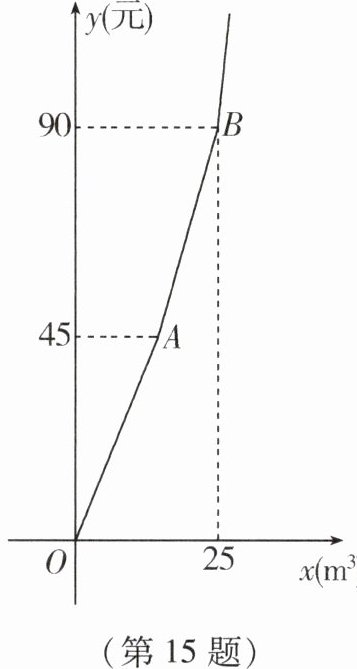
15. 为加强公民的节水意识,合理利用水资源。某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,第一、二、三级阶梯用水量的单价之比为2：3：4。如图,折线表示实行阶梯水价后每月水费y(元)与用水量$x(m^3)$之间的函数关系,其中线段AB表示第二级阶梯时y与x之间的函数关系。
(1)写出点B的实际意义；
(2)求线段AB所在直线的函数解析式；
(3)某用户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米？

答案：
(1) 当用水量为 25 $m^3$ 时, 水费为 90 元.
(2) 线段 AB 所在直线的函数解析式为 y = $\frac{9}{2}x - \frac{45}{2}$.
(3) 27 $m^3$

16. 已知一次函数y= kx+b,当-1≤x≤3时,y的取值范围为1≤y≤3,求这个一次函数的解析式。

答案： y = $\frac{1}{2}x + \frac{3}{2}$ 或 y = -$\frac{1}{2}x + \frac{5}{2}$