《2025年假日数学吉林出版集团股份有限公司八年级数学华师大版》

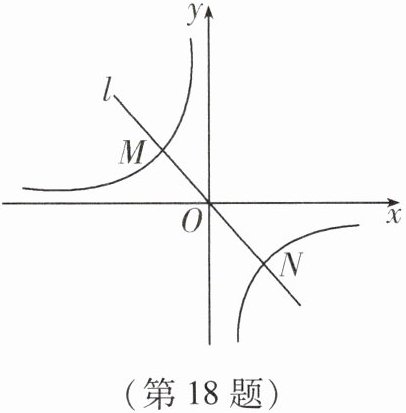
18. 如图,过原点的直线 $ l $ 与反比例函数 $ y= -\frac{1}{x} $ 的图象交于 $ M $,$ N $ 两点,根据图象猜想线段 $ MN $ 的长度的最小值.

答案： $ 2 \sqrt { 2 } $

19. 阅读下面材料：
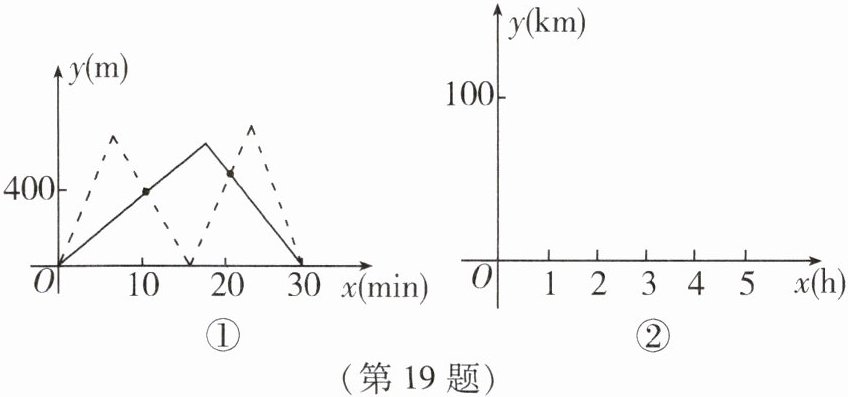
“父亲和儿子同时出去晨练. 如图①,实线表示父亲离家的距离 $ y(m) $ 与时间 $ x(min) $ 的函数关系；虚线表示儿子离家的距离 $ y(m) $ 与时间 $ x(min) $ 的函数关系. 由图象可知,他们在出发 $ 10 min $ 时第一次相遇,此时离家 $ 400 m $；晨练了 $ 30 min $,他们同时到家. ”
根据阅读材料给你的启示,利用指定的平面直角坐标系(如图②)或其他方法解答问题：
一巡逻艇和一货轮同时从 $ A $ 港口前往相距 $ 100 km $ 的 $ B $ 港口,巡逻艇和货轮的速度分别为 $ 100 km/h $ 和 $ 20 km/h $,巡逻艇不停地往返于 $ A $,$ B $ 两港口巡逻(巡逻艇掉头的时间忽略不计). 问巡逻艇与货轮何时第三次相遇？相遇时离 $ A $ 港口多远？

答案： 同时出发 $ \frac { 10 } { 3 } $ h 后两者第三次相遇，相遇时离 A 港口 $ \frac { 200 } { 3 } $ km.