《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

11. 等腰三角形的腰长为$13cm$,底边长为$10cm$,那么它的面积为______。

答案： $60\mathrm{cm}^2$

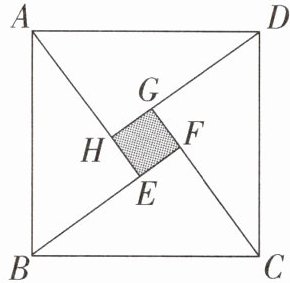
12. 如图,四个全等的直角三角形围成一个大正方形$ABCD$,中间阴影部分是一个小正方形$EFGH$,这样就组成一个“赵爽弦图”。若$AB = 5$,$AE = 4$,则正方形$EFGH$的面积为______。

答案： 1

13. 在$Rt△ABC$中,$∠C = 90^{\circ}$,$∠A$,$∠B$,$∠C的对边分别为a$,$b$,$c$。
(1)已知$a = 40$,$c = 41$,求$b$；
(2)已知$a:b = 3:4$,$c = 15$,求$b$。

答案：
(1)$b^{2}=c^{2}-a^{2}=41^{2}-40^{2}=81=9^{2}$,所以$b=9$.　
(2)设$a=3k,b=4k(k＞0)$,则$(3k)^{2}+(4k)^{2}=15^{2}$,解得$k=3$,所以$b=4×3=12$.

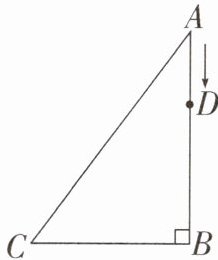
14. 如图,在$Rt△ABC$中,$∠B = 90^{\circ}$,$AB = 8cm$,$BC = 6cm$,$D点从A出发以每秒1cm的速度向B$点运动,当$D点运动到AC$的中垂线上时,运动时间为多少秒？

答案：
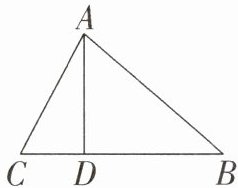
如图所示,$ED'$为$AC$的垂直平分线，连接$CD'$　　　　　　　　 　则$CD'=AD'$　在$\mathrm{Rt}\triangle BCD'$中,$CD'^{2}=BD'^{2}+BC^{2}$,　即$AD'^{2}=6^{2}+(8 - AD')^{2}$,　解得$AD'=\frac{25}{4}$,　所以当$D$点运动到$AC$的中垂线上时，运动时间为$\frac{25}{4}$秒.

15. 如图,在$△ABC$中,$AB = 20$,$BC = 21$,$AC = 13$。
(1)求$BC边上的高AD$的长；
(2)求$△ABC$的面积。

答案：
(1)设$BD=x$,则$CD=21 - x$.在$\mathrm{Rt}\triangle ABD$中,$AD^{2}=20^{2}-x^{2}$.在$\mathrm{Rt}\triangle ACD$中,$AD^{2}=13^{2}-(21 - x)^{2}$,所以$20^{2}-x^{2}=13^{2}-(21 - x)^{2}$,解得$x=16$,所以$AD=12$.　
(2)$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}×21×12=126$.

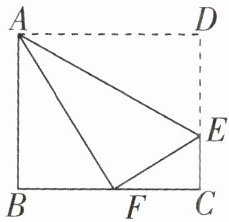
16. 如图,折叠长方形的一边$AD$,使点$D落在BC边的点F$处,已知$AB = 8cm$,$BC = 10cm$,求$CE$的长。

答案： 依题意有$\triangle ADE\cong\triangle AFE$,所以$DE=FE$,$AD=AF=BC = 10\mathrm{cm}$.在$\mathrm{Rt}\triangle ABF$中,$AB^{2}+BF^{2}=AF^{2}$,所以$BF = 6\mathrm{cm}$.又$BC = 10\mathrm{cm}$,所以$CF = 4\mathrm{cm}$.在$\mathrm{Rt}\triangle CEF$中,$EF^{2}=CE^{2}+CF^{2}$.设$CE=x$,则$DE=FE=8 - x$,所以$(8 - x)^{2}=x^{2}+4^{2}$,所以$x = 3$,即$CE = 3\mathrm{cm}$.