第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
22. (8分)观察下列等式:
$(x-1)(x+1)= x^{2}-1$;
$(x-1)(x^{2}+x+1)= x^{3}-1$;
$(x-1)(x^{3}+x^{2}+x+1)= x^{4}-1$;
$(x-1)(x^{4}+x^{3}+x^{2}+x+1)= x^{5}-1$;
……
(1)猜想$(x-1)(x^{n}+x^{n-1}+x^{n-2}+... +x+1)= $____。
(2)运用上述规律,试求:
①$2^{19}+2^{18}+2^{17}+... +2^{3}+2^{2}+2+1$;
②$5^{2025}+5^{2024}+5^{2023}+... +5^{3}+5^{2}+5+1$。
$(x-1)(x+1)= x^{2}-1$;
$(x-1)(x^{2}+x+1)= x^{3}-1$;
$(x-1)(x^{3}+x^{2}+x+1)= x^{4}-1$;
$(x-1)(x^{4}+x^{3}+x^{2}+x+1)= x^{5}-1$;
……
(1)猜想$(x-1)(x^{n}+x^{n-1}+x^{n-2}+... +x+1)= $____。
(2)运用上述规律,试求:
①$2^{19}+2^{18}+2^{17}+... +2^{3}+2^{2}+2+1$;
②$5^{2025}+5^{2024}+5^{2023}+... +5^{3}+5^{2}+5+1$。
答案:
【解析】:
本题主要考察整式的乘除以及代数式的规律识别。
(1) 通过观察给出的等式,可以发现每个等式右边的指数是左边括号内$x$的指数加1,且符号为正。
因此,可以猜想$(x-1)(x^{n}+x^{n-1}+x^{n-2}+...+x+1)=x^{n+1}-1$。
(2) ① 对于$2^{19}+2^{18}+2^{17}+...+2^{3}+2^{2}+2+1$,
可以将其看作$(2-1)$乘以这个数列,即应用
(1)中的规律,
得到$2^{20}-1$。
② 对于$5^{2025}+5^{2024}+5^{2023}+...+5^{3}+5^{2}+5+1$,
同样可以将其看作$(5-1)$乘以这个数列,
应用
(1)中的规律,得到$\frac{5^{2026}-1}{4}$。
【答案】:
(1) $x^{n+1}-1$
(2) ① $2^{20}-1$
② $\frac{5^{2026}-1}{4}$
本题主要考察整式的乘除以及代数式的规律识别。
(1) 通过观察给出的等式,可以发现每个等式右边的指数是左边括号内$x$的指数加1,且符号为正。
因此,可以猜想$(x-1)(x^{n}+x^{n-1}+x^{n-2}+...+x+1)=x^{n+1}-1$。
(2) ① 对于$2^{19}+2^{18}+2^{17}+...+2^{3}+2^{2}+2+1$,
可以将其看作$(2-1)$乘以这个数列,即应用
(1)中的规律,
得到$2^{20}-1$。
② 对于$5^{2025}+5^{2024}+5^{2023}+...+5^{3}+5^{2}+5+1$,
同样可以将其看作$(5-1)$乘以这个数列,
应用
(1)中的规律,得到$\frac{5^{2026}-1}{4}$。
【答案】:
(1) $x^{n+1}-1$
(2) ① $2^{20}-1$
② $\frac{5^{2026}-1}{4}$
23. (8分)拓广探索:若$x满足(9-x)(x-4)= 4$,求$(9-x)^{2}+(x-4)^{2}$的值。
解:设$9-x= a$,$x-4= b$,
则$(9-x)(x-4)= ab= 4$,$a+b= (9-x)+(x-4)= 5$,
所以$(9-x)^{2}+(x-4)^{2}= a^{2}+b^{2}= (a+b)^{2}-2ab= 5^{2}-2×4= 17$。
请仿照上面的方法求解问题:
(1)若$x满足(5-x)(x-2)= 2$,求$(5-x)^{2}+(x-2)^{2}$的值;
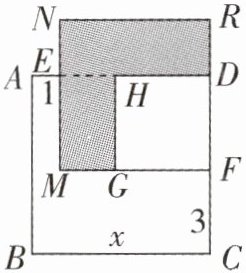
(2)已知正方形ABCD的边长为$x$,E,F分别是AD,DC上的点,且$AE= 1$,$CF= 3$,长方形EMFD的面积是48,分别以MF,DF为边作正方形,求阴影部分的面积。
解:设$9-x= a$,$x-4= b$,
则$(9-x)(x-4)= ab= 4$,$a+b= (9-x)+(x-4)= 5$,
所以$(9-x)^{2}+(x-4)^{2}= a^{2}+b^{2}= (a+b)^{2}-2ab= 5^{2}-2×4= 17$。
请仿照上面的方法求解问题:
(1)若$x满足(5-x)(x-2)= 2$,求$(5-x)^{2}+(x-2)^{2}$的值;
(2)已知正方形ABCD的边长为$x$,E,F分别是AD,DC上的点,且$AE= 1$,$CF= 3$,长方形EMFD的面积是48,分别以MF,DF为边作正方形,求阴影部分的面积。

答案:
【解析】:本题可根据所给示例的方法,通过换元法将复杂的式子进行简化,再利用完全平方公式求解。
(1)求$(5 - x)^2 + (x - 2)^2$的值
设$5 - x = a$,$x - 2 = b$。
步骤一:分析$ab$与$a + b$的值
已知$(5 - x)(x - 2) = 2$,则$ab = 2$;
$a + b=(5 - x)+(x - 2)=5 - x + x - 2 = 3$。
步骤二:计算$(5 - x)^2 + (x - 2)^2$的值
根据完全平方公式$a^2 + b^2 = (a + b)^2 - 2ab$,将$ab = 2$,$a + b = 3$代入可得:
$(5 - x)^2 + (x - 2)^2 = a^2 + b^2 = (a + b)^2 - 2ab = 3^2 - 2×2 = 9 - 4 = 5$。
(2)求阴影部分的面积
已知正方形$ABCD$的边长为$x$,$AE = 1$,$CF = 3$,长方形$EMFD$的面积是$48$。
步骤一:表示出$MF$与$DF$的长度
因为$AE = 1$,所以$DE = x - 1$;又因为$CF = 3$,所以$DF = x - 3$。
由于长方形$EMFD$的面积是$48$,且长方形面积$=$长$×$宽,所以$MF× DF = 48$,即$(x - 1)(x - 3) = 48$。
设$x - 1 = a$,$x - 3 = b$,则$ab = 48$,$a - b=(x - 1)-(x - 3)=x - 1 - x + 3 = 2$。
步骤二:计算阴影部分的面积
阴影部分的面积为$MF^2 - DF^2$,即$a^2 - b^2$。
根据平方差公式$a^2 - b^2 = (a + b)(a - b)$,先求$(a + b)^2$的值:
$(a + b)^2=(a - b)^2 + 4ab = 2^2 + 4×48 = 4 + 192 = 196$,则$a + b = \sqrt{196} = 14$(因为$a$、$b$为边长相关量,大于$0$,所以取正)。
将$a + b = 14$,$a - b = 2$代入平方差公式可得:
$a^2 - b^2 = (a + b)(a - b)=14×2 = 28$,即阴影部分的面积为$28$。
【答案】:(1)$5$;(2)$28$。
(1)求$(5 - x)^2 + (x - 2)^2$的值
设$5 - x = a$,$x - 2 = b$。
步骤一:分析$ab$与$a + b$的值
已知$(5 - x)(x - 2) = 2$,则$ab = 2$;
$a + b=(5 - x)+(x - 2)=5 - x + x - 2 = 3$。
步骤二:计算$(5 - x)^2 + (x - 2)^2$的值
根据完全平方公式$a^2 + b^2 = (a + b)^2 - 2ab$,将$ab = 2$,$a + b = 3$代入可得:
$(5 - x)^2 + (x - 2)^2 = a^2 + b^2 = (a + b)^2 - 2ab = 3^2 - 2×2 = 9 - 4 = 5$。
(2)求阴影部分的面积
已知正方形$ABCD$的边长为$x$,$AE = 1$,$CF = 3$,长方形$EMFD$的面积是$48$。
步骤一:表示出$MF$与$DF$的长度
因为$AE = 1$,所以$DE = x - 1$;又因为$CF = 3$,所以$DF = x - 3$。
由于长方形$EMFD$的面积是$48$,且长方形面积$=$长$×$宽,所以$MF× DF = 48$,即$(x - 1)(x - 3) = 48$。
设$x - 1 = a$,$x - 3 = b$,则$ab = 48$,$a - b=(x - 1)-(x - 3)=x - 1 - x + 3 = 2$。
步骤二:计算阴影部分的面积
阴影部分的面积为$MF^2 - DF^2$,即$a^2 - b^2$。
根据平方差公式$a^2 - b^2 = (a + b)(a - b)$,先求$(a + b)^2$的值:
$(a + b)^2=(a - b)^2 + 4ab = 2^2 + 4×48 = 4 + 192 = 196$,则$a + b = \sqrt{196} = 14$(因为$a$、$b$为边长相关量,大于$0$,所以取正)。
将$a + b = 14$,$a - b = 2$代入平方差公式可得:
$a^2 - b^2 = (a + b)(a - b)=14×2 = 28$,即阴影部分的面积为$28$。
【答案】:(1)$5$;(2)$28$。
查看更多完整答案,请扫码查看


