第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
22. 在$△ABC$中,$AB= AC$,点D是直线BC上一点(不与B,C重合),E是$△ABC$外一点,连接AD,AE,已知$AD= AE,∠DAE= ∠BAC$,连接CE,DE.
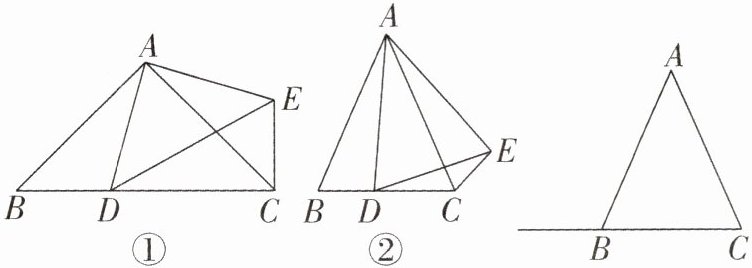
(1)如图①,点D在线段BC上,如果$∠BAC= 90^{\circ }$,则$∠ACE= $____度.
(2)如图②,当点D在线段BC上,试判断$∠ADE与∠ACE$之间的数量关系,并说明理由.
(3)当点D在线段CB的延长线上时,(2)中的结论是否成立? 若不成立,请写出新的结论并说明理由.

(1)如图①,点D在线段BC上,如果$∠BAC= 90^{\circ }$,则$∠ACE= $____度.
(2)如图②,当点D在线段BC上,试判断$∠ADE与∠ACE$之间的数量关系,并说明理由.
(3)当点D在线段CB的延长线上时,(2)中的结论是否成立? 若不成立,请写出新的结论并说明理由.
答案:
(1)45 解析:因为∠DAE=∠BAC,所以∠DAE-∠DAC=∠BAC-∠DAC,即∠BAD=∠CAE.因为 AB=AC,AD=AE,所以△BAD≌△CAE,所以∠ABD=∠ACE.因为∠BAC=90°,AB=AC,所以∠ACE=∠ABD=45°.
(2)∠ADE=∠ACE.理由如下:因为 AB=AC,AD=AE,所以∠ABC=∠ACB,∠ADE=∠AED.因为∠DAE=∠BAC,∠ABC=$\frac{1}{2}$(180°-∠BAC),∠ADE=$\frac{1}{2}$(180°-∠DAE),所以∠ABC=∠ADE.因为∠BAC=∠DAE,所以∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△BAD 和△CAE 中,$\begin{cases} AB=AC, \\ ∠BAD=∠CAE, \\ AD=AE, \end{cases}$所以△BAD≌△CAE(SAS),所以∠ABC=∠ACE,所以∠ADE=∠ACE.
(3)
(2)中的结论不成立,当点 D 在线段 CB 的延长线上时,∠ADE+∠ACE=180°.理由如下:如图所示:

因为∠DAE=∠BAC,所以∠DAE-∠BAE=∠BAC-∠BAE,即∠DAB=∠EAC,在△BAD 和△CAE 中,$\begin{cases} AB=AC, \\ ∠BAD=∠CAE, \\ AD=AE, \end{cases}$所以△BAD≌△CAE(SAS),所以∠ABD=∠ACE.因为 AB=AC,AD=AE,所以∠ABC=∠ACB,∠ADE=∠AED.因为∠DAE=∠BAC,∠ABC=$\frac{1}{2}$(180°-∠BAC),∠ADE=$\frac{1}{2}$(180°-∠DAE),所以∠ABC=∠ADE.因为∠ABD+∠ABC=180°,所以∠ADE+∠ACE=180°.
(1)45 解析:因为∠DAE=∠BAC,所以∠DAE-∠DAC=∠BAC-∠DAC,即∠BAD=∠CAE.因为 AB=AC,AD=AE,所以△BAD≌△CAE,所以∠ABD=∠ACE.因为∠BAC=90°,AB=AC,所以∠ACE=∠ABD=45°.
(2)∠ADE=∠ACE.理由如下:因为 AB=AC,AD=AE,所以∠ABC=∠ACB,∠ADE=∠AED.因为∠DAE=∠BAC,∠ABC=$\frac{1}{2}$(180°-∠BAC),∠ADE=$\frac{1}{2}$(180°-∠DAE),所以∠ABC=∠ADE.因为∠BAC=∠DAE,所以∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△BAD 和△CAE 中,$\begin{cases} AB=AC, \\ ∠BAD=∠CAE, \\ AD=AE, \end{cases}$所以△BAD≌△CAE(SAS),所以∠ABC=∠ACE,所以∠ADE=∠ACE.
(3)
(2)中的结论不成立,当点 D 在线段 CB 的延长线上时,∠ADE+∠ACE=180°.理由如下:如图所示:

因为∠DAE=∠BAC,所以∠DAE-∠BAE=∠BAC-∠BAE,即∠DAB=∠EAC,在△BAD 和△CAE 中,$\begin{cases} AB=AC, \\ ∠BAD=∠CAE, \\ AD=AE, \end{cases}$所以△BAD≌△CAE(SAS),所以∠ABD=∠ACE.因为 AB=AC,AD=AE,所以∠ABC=∠ACB,∠ADE=∠AED.因为∠DAE=∠BAC,∠ABC=$\frac{1}{2}$(180°-∠BAC),∠ADE=$\frac{1}{2}$(180°-∠DAE),所以∠ABC=∠ADE.因为∠ABD+∠ABC=180°,所以∠ADE+∠ACE=180°.
23. 我们知道,将一个正方体或长方体的表面沿某些棱剪开,可以展成一个平面图形.
(1)下列图形中,是正方体的表面展开图的是____.(单选)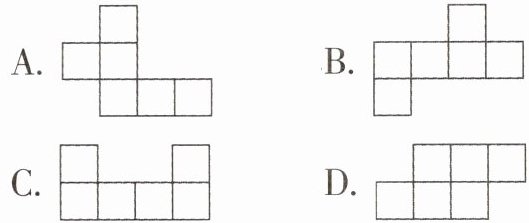
(2)如图所示的长方体,长、宽、高分别为4、3、6,若将它的表面沿某些棱剪开,展成一个平面图形. 则下列平面图形中,可能是该长方体表面展开图的有(多选)____(填序号).
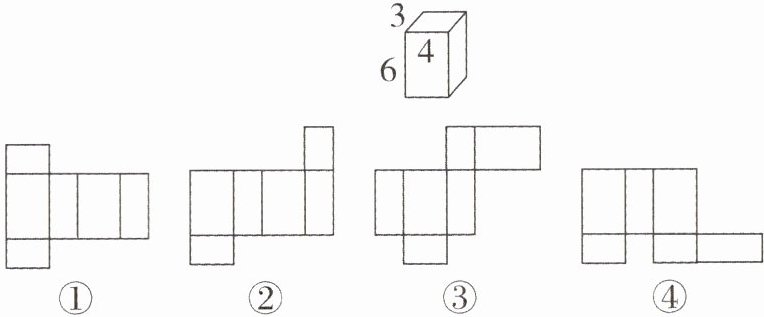
(3)如图是(2)中长方体的一种表面展开图,在图上取A,B,C三个顶点(B在线段AC上且$AB>BC$),若P,Q分别从A,C同时出发,点P以1个单位长度/秒的速度向点C运动,点Q以0.5个单位长度/秒的速度向点A运动,一个点到达终点后另一个点也停止运动,求运动多长时间时,B,P,Q三点中,有一个点正好是另两个点的中点?
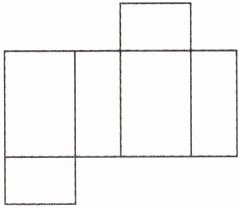
(4)事实上,(2)中长方体的表面展开图还有不少,(3)的外围周长为52,请你写出该长方体表面展开图的最大外围周长为____.
(1)下列图形中,是正方体的表面展开图的是____.(单选)

(2)如图所示的长方体,长、宽、高分别为4、3、6,若将它的表面沿某些棱剪开,展成一个平面图形. 则下列平面图形中,可能是该长方体表面展开图的有(多选)____(填序号).

(3)如图是(2)中长方体的一种表面展开图,在图上取A,B,C三个顶点(B在线段AC上且$AB>BC$),若P,Q分别从A,C同时出发,点P以1个单位长度/秒的速度向点C运动,点Q以0.5个单位长度/秒的速度向点A运动,一个点到达终点后另一个点也停止运动,求运动多长时间时,B,P,Q三点中,有一个点正好是另两个点的中点?

(4)事实上,(2)中长方体的表面展开图还有不少,(3)的外围周长为52,请你写出该长方体表面展开图的最大外围周长为____.
答案:
(1)B
(2)①②③
(3)设运动的时间为 t,如图①所示,由题意得 AB=4,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 4,点 C 在数轴上表示的数为 7,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 7-0.5t,当 B 是 PQ 的中点时,则$\frac{t+7-0.5t}{2}$=4,解得 t=2;当 P 是 BQ 的中点时,则$\frac{4+7-0.5t}{2}$=t,解得 t=$\frac{22}{5}$;当 Q 是 BP 的中点时,则$\frac{t+4}{2}$=7-0.5t,解得 t=5;

如图②所示,由题意得 AB=7,BC=4,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 7,点 C 在数轴上表示的数为 11,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 11-0.5t,当 B 是 PQ 的中点时,则$\frac{t+11-0.5t}{2}$=7,解得 t=6;当 P 是 BQ 的中点时,则$\frac{7+11-0.5t}{2}$=t,解得 t=$\frac{36}{5}$;当 Q 是 BP 的中点时,则$\frac{t+7}{2}$=11-0.5t,解得 t=$\frac{15}{2}$;

如图③所示,由题意得 AB=11,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 11,点 C 在数轴上表示的数为 14,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 14-0.5t,当 B 是 PQ 的中点时,则$\frac{t+14-0.5t}{2}$=11,解得 t=16(舍去);当 P 是 BQ 的中点时,则$\frac{11+14-0.5t}{2}$=t,解得 t=10;当 Q 是 BP 的中点时,则$\frac{t+11}{2}$=14-0.5t,解得 t=$\frac{17}{2}$;

如图④所示,由题意得 AB=7,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 7,点 C 在数轴上表示的数为 10,所以运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 10-0.5t,当 B 是 PQ 的中点时,则$\frac{t+10-0.5t}{2}$=7,解得 t=8;当 P 是 BQ 的中点时,则$\frac{7+10-0.5t}{2}$=t,解得 t=$\frac{34}{5}$;当 Q 是 BP 的中点时,则$\frac{7+t}{2}$=10-0.5t,解得 t=$\frac{13}{2}$;

如图⑤所示,由题意得 AB=6,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 6,点 C 在数轴上表示的数为 9,所以运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 9-0.5t,当 B 是 PQ 的中点时,则$\frac{t+9-0.5t}{2}$=6,解得 t=6;当 P 是 BQ 的中点时,则$\frac{6+9-0.5t}{2}$=t,解得 t=6;当 Q 是 BP 的中点时,则$\frac{t+6}{2}$=9-0.5t,解得 t=6(这三种情况下,B,P,Q 三点重合,不符合题意).

综上所述,当运动时间为 2 秒或$\frac{22}{5}$秒或 5 秒或 6 秒或$\frac{36}{5}$秒或$\frac{15}{2}$秒或 10 秒或$\frac{17}{2}$秒或 8 秒或$\frac{34}{5}$秒或$\frac{13}{2}$秒时,B,P,Q 三点中,有一个点正好是另两个点的中点.
(4)70 解析:外围周长最大的表面展开图,如图⑥:

观察展开图可知,外围周长为 6×8 + 4×4 + 3×2 = 70.
(1)B
(2)①②③
(3)设运动的时间为 t,如图①所示,由题意得 AB=4,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 4,点 C 在数轴上表示的数为 7,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 7-0.5t,当 B 是 PQ 的中点时,则$\frac{t+7-0.5t}{2}$=4,解得 t=2;当 P 是 BQ 的中点时,则$\frac{4+7-0.5t}{2}$=t,解得 t=$\frac{22}{5}$;当 Q 是 BP 的中点时,则$\frac{t+4}{2}$=7-0.5t,解得 t=5;

如图②所示,由题意得 AB=7,BC=4,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 7,点 C 在数轴上表示的数为 11,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 11-0.5t,当 B 是 PQ 的中点时,则$\frac{t+11-0.5t}{2}$=7,解得 t=6;当 P 是 BQ 的中点时,则$\frac{7+11-0.5t}{2}$=t,解得 t=$\frac{36}{5}$;当 Q 是 BP 的中点时,则$\frac{t+7}{2}$=11-0.5t,解得 t=$\frac{15}{2}$;

如图③所示,由题意得 AB=11,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 11,点 C 在数轴上表示的数为 14,运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 14-0.5t,当 B 是 PQ 的中点时,则$\frac{t+14-0.5t}{2}$=11,解得 t=16(舍去);当 P 是 BQ 的中点时,则$\frac{11+14-0.5t}{2}$=t,解得 t=10;当 Q 是 BP 的中点时,则$\frac{t+11}{2}$=14-0.5t,解得 t=$\frac{17}{2}$;

如图④所示,由题意得 AB=7,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 7,点 C 在数轴上表示的数为 10,所以运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 10-0.5t,当 B 是 PQ 的中点时,则$\frac{t+10-0.5t}{2}$=7,解得 t=8;当 P 是 BQ 的中点时,则$\frac{7+10-0.5t}{2}$=t,解得 t=$\frac{34}{5}$;当 Q 是 BP 的中点时,则$\frac{7+t}{2}$=10-0.5t,解得 t=$\frac{13}{2}$;

如图⑤所示,由题意得 AB=6,BC=3,设点 A 在数轴上表示的数为 0,点 B 在数轴上表示的数为 6,点 C 在数轴上表示的数为 9,所以运动 t 秒后,点 P 在数轴上表示的数为 t,点 Q 在数轴上表示的数为 9-0.5t,当 B 是 PQ 的中点时,则$\frac{t+9-0.5t}{2}$=6,解得 t=6;当 P 是 BQ 的中点时,则$\frac{6+9-0.5t}{2}$=t,解得 t=6;当 Q 是 BP 的中点时,则$\frac{t+6}{2}$=9-0.5t,解得 t=6(这三种情况下,B,P,Q 三点重合,不符合题意).

综上所述,当运动时间为 2 秒或$\frac{22}{5}$秒或 5 秒或 6 秒或$\frac{36}{5}$秒或$\frac{15}{2}$秒或 10 秒或$\frac{17}{2}$秒或 8 秒或$\frac{34}{5}$秒或$\frac{13}{2}$秒时,B,P,Q 三点中,有一个点正好是另两个点的中点.
(4)70 解析:外围周长最大的表面展开图,如图⑥:

观察展开图可知,外围周长为 6×8 + 4×4 + 3×2 = 70.
查看更多完整答案,请扫码查看


