第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
9. 在同一年出生的367名学生中,至少有两人的生日是同一天是______(填“必然事件”“随机事件”或“不可能事件”).
答案:
必然事件
10. 掷一枚骰子,偶数点朝上的可能性______奇数点朝上的可能性.(填“>”“=”或“<”)
答案:
=
11. 在科学课外活动中,小明同学在相同的条件下做了某种作物种子发芽的试验,结果如下表所示:
|种子数/个|100|200|300|400|
|发芽种子数/个|94|187|282|376|
由此估计这种种子作物发芽率约为______(精确到0.01).
|种子数/个|100|200|300|400|
|发芽种子数/个|94|187|282|376|
由此估计这种种子作物发芽率约为______(精确到0.01).
答案:
0.94
12. 甲、乙两人玩游戏,把一个均匀的小正方体的每个面上分别标上数字1,2,3,4,5,6,任意掷出小正方体后,若朝上的数字比3大,则甲胜;若朝上的数字比3小,则乙胜.这个游戏对甲、乙双方公平吗?______.
答案:
不公平
13. 从长度为1cm、2cm、4cm、6cm、7cm、8cm的6根木棒中随机抽取一根,能与长度分别为3cm和5cm的木棒围成三角形的概率为______.
答案:
$\frac{1}{2}$
14. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为______.
答案:
12
15. 如图,A,B是数轴上的两点,在线段AB上任取一点C,则点C到原点的距离不大于2的概率是______.
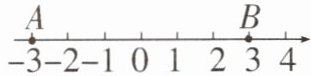
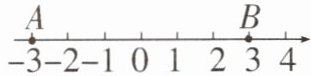
答案:
$\frac{2}{3}$
16. 如图,△ABC的面积为$10cm^2,BP$平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形内有一点M,则点M落在△BPC内(包括边界)的概率为______.
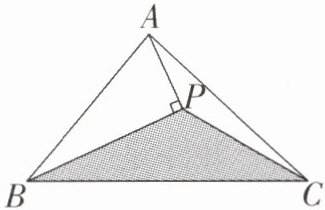

答案:
$\frac{1}{2}$
17. (6分)在一个不透明的口袋中装有大小、形状完全相同的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了,请判断以下事件是不确定事件、不可能事件还是必然事件.
(1)从口袋中一次任意取出1个球,是白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任取5个球,只有蓝球和白球,没有红球;
(4)从口袋中一次任意取出6个球,恰好红、蓝、白三种颜色的球都齐了.
(1)从口袋中一次任意取出1个球,是白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任取5个球,只有蓝球和白球,没有红球;
(4)从口袋中一次任意取出6个球,恰好红、蓝、白三种颜色的球都齐了.
答案:
(1)可能发生,也可能不发生,故是不确定事件.
(2)一定不会发生,故是不可能事件.
(3)可能发生,也可能不发生,故是不确定事件.
(4)可能发生,也可能不发生,故是不确定事件.
(1)可能发生,也可能不发生,故是不确定事件.
(2)一定不会发生,故是不可能事件.
(3)可能发生,也可能不发生,故是不确定事件.
(4)可能发生,也可能不发生,故是不确定事件.
查看更多完整答案,请扫码查看


