《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

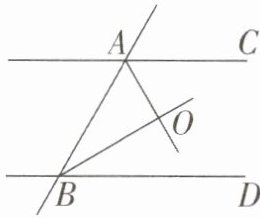
8. 如图,直线$ AC // BD $,AO,BO分别是$ \angle BAC $,$ \angle ABD $的平分线,那么$ \angle BAO 与 \angle ABO $之间的大小关系一定为( )

A.互余

B.相等
C.互补
D.不等

答案： 【解析】：根据题目已知条件，直线$AC$平行于$BD$，$AO$是$\angle BAC$的平分线，$BO$是$\angle ABD$的平分线。
根据平行线的性质，当两直线平行时，它们之间的交替内角是相等的。所以，$\angle BAC + \angle ABD = 180^\circ$。
由于$AO$是$\angle BAC$的平分线，根据角的平分线的性质，可得$\angle BAO = \frac{1}{2} \angle BAC$。
同理，由于$BO$是$\angle ABD$的平分线，可得$\angle ABO = \frac{1}{2} \angle ABD$。
因此，$\angle BAO + \angle ABO = \frac{1}{2} \angle BAC + \frac{1}{2} \angle ABD = \frac{1}{2} (\angle BAC + \angle ABD) = \frac{1}{2} × 180^\circ = 90^\circ$。
由于$\angle BAO$和$\angle ABO$的和为$90^\circ$，根据互余角的定义（两个角的和为$90^\circ$），可以得出$\angle BAO$与$\angle ABO$是互余的。
【答案】：A

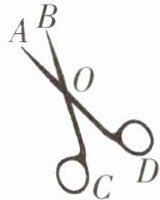
9. 如图,当剪刀口$ \angle AOB 增大 15^{\circ} $时,则$ \angle COD $增大______.

答案： 【解析】：
由题目的描述和图示可知，$\angle AOB$和$\angle COD$是对顶角，对顶角相等，并且它们同时变化。
因此，当$\angle AOB$增大$15^{\circ}$时，$\angle COD$也增大同样的度数，即$15^{\circ}$。
【答案】：
$15^{\circ}$

10. 已知$ \angle \alpha $是它的余角的2倍,则$ \angle \alpha = $______.

答案： 【解析】：
本题主要考查余角的概念及线性方程的解法。
余角是指两个角的和为$90^\circ$。
根据题意，设角$\alpha$的余角为$90^\circ - \alpha$，则有$\alpha = 2(90^\circ - \alpha)$。
现在，解这个方程以找出$\alpha$的值。
【答案】：
解：
根据余角的定义和题目条件，可以列出方程：
$\alpha = 2(90^\circ - \alpha)$，
展开方程得：
$\alpha = 180^\circ - 2\alpha$，
移项并合并同类项：
$3\alpha = 180^\circ$，
解得：
$\alpha = 60^\circ$。
故答案为：$60^\circ$。

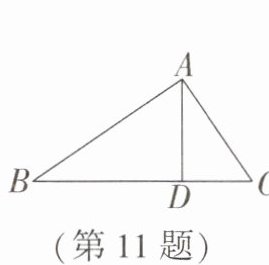
11. 如图,$ AB \perp AC $,$ AD \perp BC $,能表示点到直线的距离的线段有______条.

答案： 解：4

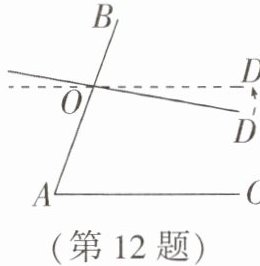
12. 如图,$ \angle A = 70^{\circ} $,O是AB上一点,直线OD与AB所夹的$ \angle AOD = 100^{\circ} $,要使$ OD // AC $,直线OD绕点O按逆时针方向至少旋转______.

答案： 解：要使 $ OD // AC $，根据两直线平行，同旁内角互补，可得 $ \angle AOD' + \angle A = 180^{\circ} $（设旋转后OD的位置为OD'）。
已知 $ \angle A = 70^{\circ} $，则 $ \angle AOD' = 180^{\circ} - 70^{\circ} = 110^{\circ} $。
原来 $ \angle AOD = 100^{\circ} $，所以旋转的角度为 $ 110^{\circ} - 100^{\circ} = 10^{\circ} $。
10°

13. 如图,直线AB,CD,EF相交于点O,$ \angle AOE = 30^{\circ} $,$ \angle BOC = 2 \angle AOC $,则$ \angle DOF = $______.

答案： 解：设∠AOC = x，则∠BOC = 2x。
因为∠AOC + ∠BOC = 180°，
所以x + 2x = 180°，解得x = 60°，即∠AOC = 60°。
因为∠AOE = 30°，
所以∠COE = ∠AOC - ∠AOE = 60° - 30° = 30°。
因为∠DOF与∠COE是对顶角，
所以∠DOF = ∠COE = 30°。
30°

14. 如图,已知$ AB // CD $,$ \angle ABE = 100^{\circ} $,$ \angle BEC = 40^{\circ} $,则$ \angle ECD $的度数为______.

答案： 解：过点E作EF//AB。
因为AB//CD，所以EF//CD。
因为AB//EF，∠ABE=100°，所以∠BEF=180°-∠ABE=180°-100°=80°。
因为∠BEC=40°，所以∠FEC=∠BEF-∠BEC=80°-40°=40°。
因为EF//CD，所以∠ECD=∠FEC=40°。
40°

15. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则$ \angle ABC + \angle BCD = $______度.

答案： 【解析】：本题可根据平行线的性质以及四边形内角和定理来求解$\angle ABC + \angle BCD$的度数。
步骤一：过点$B$作$BF// AE$
因为$CD// AE$，$BF// AE$，根据平行公理的推论：平行于同一条直线的两条直线互相平行，所以$CD// BF$。
步骤二：利用平行线的性质得到相关角的关系
因为$BA\perp AE$，$BF// AE$，所以$\angle ABF = 90^{\circ}$（两直线平行，同旁内角互补）。
由于$CD// BF$，根据两直线平行，同旁内角互补，可得$\angle BCD + \angle CBF = 180^{\circ}$。
步骤三：求$\angle ABC + \angle BCD$的度数
$\angle ABC + \angle BCD = \angle ABF + \angle FBC + \angle BCD$，将$\angle ABF = 90^{\circ}$，$\angle BCD + \angle CBF = 180^{\circ}$代入可得：
$\angle ABC + \angle BCD = 90^{\circ} + 180^{\circ} = 270^{\circ}$。
【答案】：$270$

16. 如图,把一张长方形纸条ABCD沿EF折叠,若$ \angle 1 = 58^{\circ} $,则$ \angle AEG = $______.

答案： 解：
∵四边形ABCD是长方形，
∴AD//BC，
∴∠DEF=∠1=58°，
由折叠的性质得：∠GEF=∠DEF=58°，
∵∠AEG+∠GEF+∠DEF=180°，
∴∠AEG=180°-∠GEF-∠DEF=180°-58°-58°=64°。
故答案为：64°。

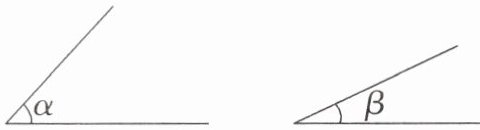
17. (6分)如图,已知$ \angle \alpha 和 \angle \beta $.利用尺规作图,求作$ \angle AOC $,使$ \angle AOC = \angle \alpha - \angle \beta $.

答案： 【解析】：
本题考查尺规作图作一个角等于已知角以及角的和差关系，需要先作出一个角等于$\angle\alpha$，再在其内部以这个角的一边为边作一个角等于$\angle\beta$，两角的差即为所求$\angle AOC$。
【答案】：
解：
1. 作$\angle AOB = \angle\alpha$。
以点$O$为圆心，任意长为半径画弧，分别交$\angle\alpha$的两边于点$M$、$N$。
以点$O$为圆心，同样长为半径画弧，交$OA$于点$P$。
以点$P$为圆心，$MN$长为半径画弧，与前弧交于点$Q$，连接$OQ$并延长，则$\angle AOB = \angle\alpha$。
2. 在$\angle AOB$内部，以$OB$为一边作$\angle BOC = \angle\beta$。
以点$O$为圆心，任意长为半径画弧，交$\angle\beta$的两边于点$S$、$T$。
以点$O$为圆心，同样长为半径画弧，交$OB$于点$R$。
以点$R$为圆心，$ST$长为半径画弧，与前弧交于点$U$，连接$OU$并延长，则$\angle BOC = \angle\beta$。
3. 此时$\angle AOC = \angle AOB - \angle BOC = \angle\alpha - \angle\beta$。
图略。