《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

12. 将若干张长为$40cm$,宽为$15cm$的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为$5cm$,则$n$张白纸粘合后的总长度为______$cm$。(用含$n$的代数式表示)

答案： (35n+5)

13. 有一组按规律排列的式子：$a^{2}$,$\frac{a^{4}}{3}$,$\frac{a^{6}}{5}$,$\frac{a^{8}}{7}$,…,则第$n$个式子是______。

答案： $\frac{a^{2n}}{2n - 1}$

14. 若$x + y = 3$,$xy = 2$,则$(5x + 2)-(3xy - 5y)= $______。

答案： 11

15. 如果$x = 1$时,代数式$2ax^{3}+3bx + 4的值是5$,那么$x = -1$时,代数式$2ax^{3}+3bx + 4$的值是______。

答案： 3

16. 如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第$n$个图案中白色正方形比黑色正方形多______个。(用含$n$的代数式表示)

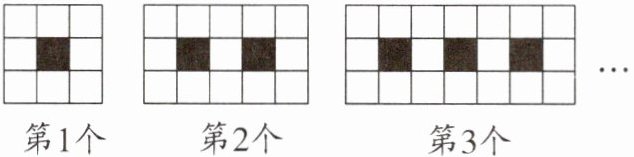
答案： 4n+3

17. (8分)化简：
(1)$3y^{2}-1-2y - 5 + 3y - y^{2}$；
(2)$3(4mn - m^{2})-4mn - 2(3mn - m^{2})$。

答案：
(1)$3y^{2}-1-2y-5+3y-y^{2}=2y^{2}+y-6$.
(2)$3(4mn - m^{2})-4mn-2(3mn - m^{2})=12mn - 3m^{2}-4mn - 6mn + 2m^{2}=2mn - m^{2}$.

18. (6分)先化简,再求值：$\frac{2}{3}a^{2}-2(2a+\frac{1}{2}b)-(\frac{5}{3}a^{2}-a-\frac{3}{2}b)$,其中$a = -1$,$b = 2$。

答案： $\frac{2}{3}a^{2}-2(2a+\frac{1}{2}b)-(\frac{5}{3}a^{2}-a-\frac{3}{2}b)=\frac{2}{3}a^{2}-4a - b-\frac{5}{3}a^{2}+a+\frac{3}{2}b=-a^{2}-3a+\frac{1}{2}b$,当a = -1,b = 2时,原式$=-(-1)^{2}-3×(-1)+\frac{1}{2}×2=3$.

19. (6分)课堂上李老师给出了一道整式求值的题目,李老师把要求的整式$(7a^{3}-6a^{3}b + 3a^{2}b)-(-3a^{3}-6a^{3}b + 3a^{2}b + 10a^{3}-3)$写完后,让王红同学顺便给出一组$a$,$b$的值,老师自己说答案,当王红说完：“$a = 65$,$b = -2025$”后,李老师不假思索,立刻就说出答案“$3$”。同学们觉得不可思议,但李老师用坚定的口吻说：“这个答案准确无误。”李老师说的对吗？你能说出其中的道理吗？

答案： 对.$(7a^{3}-6a^{3}b+3a^{2}b)-(-3a^{3}-6a^{3}b+3a^{2}b+10a^{3}-3)=7a^{3}-6a^{3}b+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+3=(7a^{3}+3a^{3}-10a^{3})+(-6a^{3}b+6a^{3}b)+(3a^{2}b-3a^{2}b)+3=3$,所以不管a,b取何值，整式的值都为3.