第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
21. (8分)公园门票价格规定如下表:
某校七年级(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.
经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才更省钱?
某校七年级(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.
经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才更省钱?
答案:
(1)设七年级
(1)班有x人,则有13x+11(104-x)=1240或13x+9(104-x)=1240,解得x=48或x=76(不合题意,舍去).故七年级
(1)班有48人,七年级
(2)班有56人.
(2)1240-104×9=304(元),即可省304元.
(3)由
(1)可知七年级
(1)班有48人,要想享受优惠,多买3张票需要51×11=561(元),48×13=624(元)>561元,故48人买51张票可以更省钱.
(1)设七年级
(1)班有x人,则有13x+11(104-x)=1240或13x+9(104-x)=1240,解得x=48或x=76(不合题意,舍去).故七年级
(1)班有48人,七年级
(2)班有56人.
(2)1240-104×9=304(元),即可省304元.
(3)由
(1)可知七年级
(1)班有48人,要想享受优惠,多买3张票需要51×11=561(元),48×13=624(元)>561元,故48人买51张票可以更省钱.
22. (8分)已知:有理数$a$,$b$,$c$在数轴上的位置如图所示,且$|c| > |a|$.
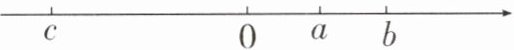
(1)化简:$|b - c| - |c - 3a| + |2a + b|$.
(2)若$|a + 10| = 20$,$b^{2} = 400$,$c$的相反数是30,求$a$,$b$,$c$的值.
(3)在(2)的条件下,$a$,$b$,$c分别是点A$,$B$,$C$在数轴上所对应的数,数轴上是否存在一点$P$,使得$P点到C点的距离加上P点到A点的距离减去P点到B$点的距离为50,即$PC + PA - PB = 50$?若存在,求出$P$点在数轴上所对应的数;若不存在,请说明理由.
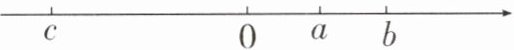
(1)化简:$|b - c| - |c - 3a| + |2a + b|$.
(2)若$|a + 10| = 20$,$b^{2} = 400$,$c$的相反数是30,求$a$,$b$,$c$的值.
(3)在(2)的条件下,$a$,$b$,$c分别是点A$,$B$,$C$在数轴上所对应的数,数轴上是否存在一点$P$,使得$P点到C点的距离加上P点到A点的距离减去P点到B$点的距离为50,即$PC + PA - PB = 50$?若存在,求出$P$点在数轴上所对应的数;若不存在,请说明理由.
答案:
(1)观察数轴,可知c<0,a>0,b>0,所以b-c>0,c-3a<0,2a+b>0,所以原式=(b-c)-(3a-c)+(2a+b)=2b-a.
(2)因为|a+10|=20,a>0,所以a=10.因为b²=400,b>0,所以b=20.因为c的相反数是30,所以c=-30.
(3)设P点在数轴上所对应的数为x.当x<-30时,有-30-x+(10-x)-(20-x)=50,解得x=-90;当-30≤x≤10时,有x-(-30)+(10-x)-(20-x)=50,解得x=30(舍去);当10<x≤20时,有x-(-30)+(x-10)-(20-x)=50,解得x=50/3;当x>20时,有x-(-30)+(x-10)-(x-20)=50,解得x=10(舍去).综上所述,数轴上存在一点P,使得PC+PA-PB=50,符合条件のP点在数轴上所对应的数为-90或50/3.
(1)观察数轴,可知c<0,a>0,b>0,所以b-c>0,c-3a<0,2a+b>0,所以原式=(b-c)-(3a-c)+(2a+b)=2b-a.
(2)因为|a+10|=20,a>0,所以a=10.因为b²=400,b>0,所以b=20.因为c的相反数是30,所以c=-30.
(3)设P点在数轴上所对应的数为x.当x<-30时,有-30-x+(10-x)-(20-x)=50,解得x=-90;当-30≤x≤10时,有x-(-30)+(10-x)-(20-x)=50,解得x=30(舍去);当10<x≤20时,有x-(-30)+(x-10)-(20-x)=50,解得x=50/3;当x>20时,有x-(-30)+(x-10)-(x-20)=50,解得x=10(舍去).综上所述,数轴上存在一点P,使得PC+PA-PB=50,符合条件のP点在数轴上所对应的数为-90或50/3.
查看更多完整答案,请扫码查看


