《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

18. (6分)如图所示,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案：

方案一：分别过点C,D作AB的垂线,垂足分别为E,F,沿CE,DF铺设管道；
方案二：连接CD交AB于点P,沿PC,PD铺设管道.
按哪一种方案铺设管道更节省材料？为什么？(忽略河流的宽度)

答案： 【解析】：本题可根据垂线段最短的性质来判断哪种方案铺设管道更节省材料。
垂线段最短的性质为：从直线外一点到这条直线所作的垂线段最短。
在方案一中，分别过点$C$，$D$作$AB$的垂线，垂足分别为$E$，$F$，沿$CE$，$DF$铺设管道，此时$CE$是点$C$到直线$AB$的垂线段，$DF$是点$D$到直线$AB$的垂线段。
在方案二中，连接$CD$交$AB$于点$P$，沿$PC$，$PD$铺设管道，$PC$与$PD$不是点$C$、$D$到直线$AB$的垂线段。
根据垂线段最短可知，$CE\lt PC$，$DF\lt PD$，所以方案一中铺设管道的长度$CE + DF$比方案二中铺设管道的长度$PC + PD$更短，即方案一更节省材料。
【答案】：方案一铺设管道更节省材料。理由如下：
因为垂线段最短，方案一中$CE$是点$C$到直线$AB$的垂线段，$DF$是点$D$到直线$AB$的垂线段；方案二中$PC$与$PD$不是点$C$、$D$到直线$AB$的垂线段。
所以$CE\lt PC$，$DF\lt PD$，则$CE + DF\lt PC + PD$，即方案一铺设管道更节省材料。

19. (8分)如图所示,已知$ \angle 1 + \angle 2 = 180^{\circ} $,$ \angle A = \angle C $,DA平分$ \angle BDF $,那么BC平分$ \angle DBE $吗？为什么？

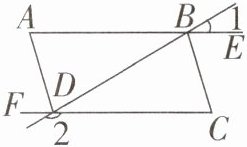
答案： 解：BC平分∠DBE，理由如下：
∵∠1+∠2=180°，∠1=∠ABD（对顶角相等）
∴∠ABD+∠2=180°
∴AB//CF（同旁内角互补，两直线平行）
∴∠A=∠ADF（两直线平行，内错角相等）
∵∠A=∠C
∴∠ADF=∠C
∴AD//BC（同位角相等，两直线平行）
∴∠ADB=∠DBC（两直线平行，内错角相等），∠FDA=∠CBE（两直线平行，同位角相等）
∵DA平分∠BDF
∴∠FDA=∠ADB
∴∠CBE=∠DBC
即BC平分∠DBE

20. (8分)将一副三角板拼成如图所示的图形,过点C作CF平分$ \angle DCE $交DE于点F.
(1)CF与AB平行吗？为什么？
(2)求$ \angle DFC $的度数.

答案：
(1)CF与AB平行。
解：因为CF平分∠DCE，∠DCE=90°，所以∠1=∠2=45°。
又因为∠3=45°，所以∠1=∠3。
所以CF//AB（内错角相等，两直线平行）。
(2)解：在△DFC中，∠D=30°，∠2=45°，
所以∠DFC=180°-∠D-∠2=180°-30°-45°=105°。