《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

16. 如图,观察“田”字中各数之间的关系：

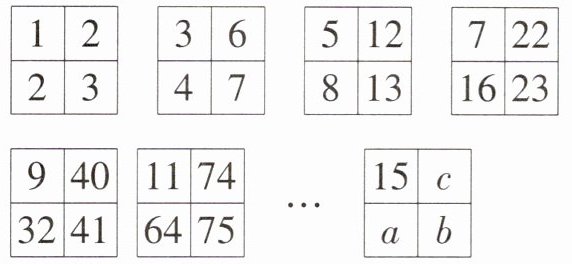
则$c$的值为______。

答案： 270 解析:经过观察，每个“田”左上角数字依此是1,3,5,7等奇数，此位置数为15时，恰好是第8个奇数，即此“田”字为第8个。观察每个“田”字左下角数据，可以发现，规律是$2,2^{2},2^{3},2^{4}$等，则第8个“田”字左下角的数为$2^{8}$。观察左下角和右上角，每个“田”字的右上角数字依次比左下角多0,2,4,6等，到第8个“田”字右上角数字比左下角多14，则$c = 2^{8}+14 = 270$。

17. 观察下列各个等式的规律：
第一个等式是$\frac{2^2 - 1^2 - 1}{2} = 1$,第二个等式是$\frac{3^2 - 2^2 - 1}{2} = 2$,第三个等式是$\frac{4^2 - 3^2 - 1}{2} = 3$,…。
请用上述等式反映出的规律解决下列问题：
(1)直接写出第四个等式；
(2)猜想第$n$个等式(用含$n$的代数式表示),并证明你猜想的等式是正确的。

答案：
(1)由题目中式子的变化规律可得，第四个等式是$\frac{5^2 - 4^2 - 1}{2} = 4$。
(2)猜想第n个等式是$\frac{(n + 1)^2 - n^2 - 1}{2} = n$，证明:因为$\frac{(n + 1)^2 - n^2 - 1}{2}=\frac{[(n + 1)+n][(n + 1)-n]-1}{2}=\frac{2n + 1 - 1}{2}=\frac{2n}{2}=n$，所以第n个等式是$\frac{(n + 1)^2 - n^2 - 1}{2} = n$。

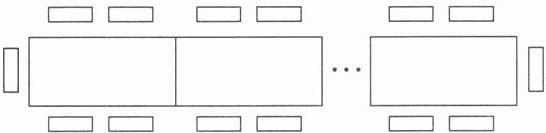
18. 一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接。
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人？
(2)若用餐的人数有90人,则这样的餐桌需要多少张？

答案：
(1)根据图中的规律我们可以发现，每多拼接一张餐桌，可坐的人数就增多4人。即拼接x张餐桌四周可以坐$6 + 4(x - 1)=(4x + 2)$人。所以，拼4张可以坐$4×4 + 2 = 18$人，拼8张可以坐$4×8 + 2 = 34$人。
(2)由题意可知$4x + 2 = 90$，解得$x = 22$。故这样的餐桌需要22张。

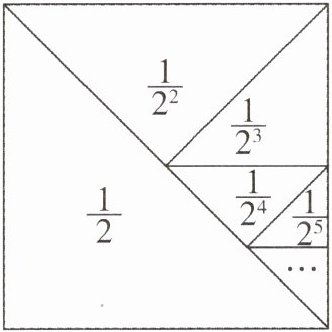
19. 数学活动中,小明为了求$\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + … + \frac{1}{2^n}$的值,设计了如图所示的几何图形。
(1)求$\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + … + \frac{1}{2^n}$的值；
(2)请你设计其他的图形求$\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + … + \frac{1}{2^n}$的值。

答案：

(1)由图形可得:$\frac{1}{2}=1-\frac{1}{2}$；$\frac{1}{2}+\frac{1}{2^2}=\frac{3}{4}=1-\frac{1}{2^2}$；$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}=\frac{7}{8}=1-\frac{1}{2^3}$；…所以$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^n}=1-\frac{1}{2^n}$。
(2)答案不唯一，如图: