第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
8. 如图,信用卡上的号码由 14 位数字组成,每一位数字写在下面的方格中,如果任何相邻的三个数字之和都等于 20,则$x$的值等于( )
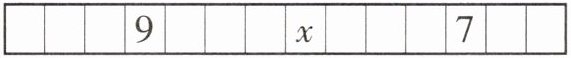
A.3
B.4
C.5
D.6
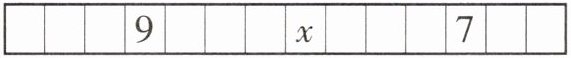
A.3
B.4
C.5
D.6
答案:
B
9. 如果关于$x的方程(a^2 - 1)x = a + 1$无解,那么$a = $______.
答案:
1
10. 若$a$,$b$互为相反数,$c$,$d$互为倒数,$p$的绝对值等于 2,则关于$x的方程(a + b)x^2 + 3cd \cdot x - p^2 = 0的解为x = $______.
答案:
$\frac{4}{3}$
11. 若$(m - 3)x^{|m| - 2} + 1 = - 5是关于x$的一元一次方程,则$m = $______;方程的解为______.
答案:
-3 $x=1$
12. 若关于$x的方程2mx + 3m = 1与3x + 6x = - 3$的解相同,则$m$的值为______.
答案:
$\frac{3}{7}$
13. 一个直径为 90 毫米的圆柱形玻璃杯中装满了水,把杯中的水倒入一个底面积为$131 × 131$平方毫米、高为 81 毫米的长方体铁盒中,当铁盒装满水时,玻璃杯中水的高度大约下降了多少?设大约下降了$x$毫米,则可列方程为______.
答案:
$\pi\left(\frac{90}{2}\right)^2x=131^2×81$
14. 某项工作,甲单独做需 20 h 完成,乙单独做需 12 h 完成,现在先由甲单独做 4 h,剩下的部分由甲、乙合做完成. 设甲、乙合做的时间为$x$h 时,可列方程为______.
答案:
$\frac{4+x}{20}+\frac{x}{12}=1$
15. 有一系列方程:第 1 个方程是$x + \frac{x}{2} = 3$,解为$x = 2$;第 2 个方程是$\frac{x}{2} + \frac{x}{3} = 5$,解为$x = 6$;第 3 个方程是$\frac{x}{3} + \frac{x}{4} = 7$,解为$x = 12$;…$$. 根据规律,第 10 个方程是______,其解为______.
答案:
$\frac{x}{10}+\frac{x}{11}=21$ $x=110$
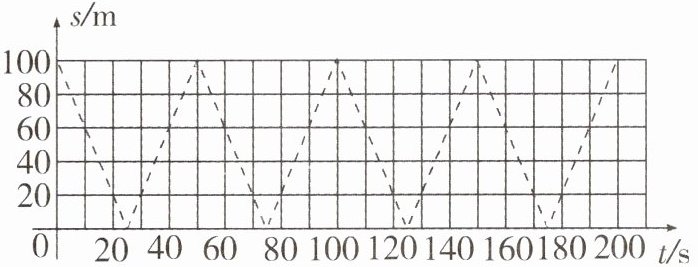
16. 甲、乙两人在 100 米直道$AB$上练习匀速往返跑,若甲、乙分别从$A$,$B$两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为 5 m/s 和 4 m/s. 乙离$A端的距离s$(单位:m)与运动时间$t$(单位:s)之间的关系$(0 \leq t \leq 200)$如图虚线所示,则甲、乙两人第 7 次相遇时$t$的值是______.

答案:
$\frac{1300}{9}$ 解析:甲和乙第1次相遇时,两人所跑路程之和为100米,甲和乙第2次相遇时,两人所跑路程之和为$100×2+100=300$(米),甲和乙第3次相遇时,两人所跑路程之和为$200×2+100=500$(米),甲和乙第4次相遇时,两人所跑路程之和为$300×2+100=700$(米)……甲和乙第7次相遇时,两人所跑路程之和为$600×2+100=1300$(米).根据题意,得$1300=(5+4)t$,解得$t=\frac{1300}{9}$.
17. 解方程:
(1)$(x - 2) - 10 = - (x + 6)$;
(2)$2(x - 3) = 5 - 3(x + 1)$;
(3)$x - \frac{x - 2}{5} = \frac{2x - 5}{3} - 3$;
(4)$\frac{0.2x + 0.7}{0.5} - \frac{0.03x - 0.05}{0.04} = 1$.
(1)$(x - 2) - 10 = - (x + 6)$;
(2)$2(x - 3) = 5 - 3(x + 1)$;
(3)$x - \frac{x - 2}{5} = \frac{2x - 5}{3} - 3$;
(4)$\frac{0.2x + 0.7}{0.5} - \frac{0.03x - 0.05}{0.04} = 1$.
答案:
(1)$x=3$.
(2)$x=1.6$.
(3)$x=-38$.
(4)$x=\frac{33}{7}$.
(1)$x=3$.
(2)$x=1.6$.
(3)$x=-38$.
(4)$x=\frac{33}{7}$.
查看更多完整答案,请扫码查看


