第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
20. 根据下表素材,完成表中的任务.
| 素材1 | 某校重视学生的课外体育活动,打算在某商店采购一批篮球和跳绳,已知篮球的单价比跳绳的单价的5倍多10元,购买2个篮球与购买11条跳绳所花的钱一样多. |
| 素材2 | 该商店给学校提供以下两种优惠方案:方案①:篮球和跳绳都按单价的八五折付款;方案②:买一个篮球送一条跳绳.现学校要购买篮球30个,跳绳$ a(a > 30) $条. |
| 任务1 | (1)求篮球的单价与跳绳的单价各是多少. |
| 任务2 | (2)当购买多少条跳绳时,使用方案①、方案②购买篮球和跳绳的总费用相同? |
| 任务3 | (3)若两种优惠方案可同时使用,当$ a = 60 $时,请你通过计算给出更省钱的购买方案. |
| 素材1 | 某校重视学生的课外体育活动,打算在某商店采购一批篮球和跳绳,已知篮球的单价比跳绳的单价的5倍多10元,购买2个篮球与购买11条跳绳所花的钱一样多. |
| 素材2 | 该商店给学校提供以下两种优惠方案:方案①:篮球和跳绳都按单价的八五折付款;方案②:买一个篮球送一条跳绳.现学校要购买篮球30个,跳绳$ a(a > 30) $条. |
| 任务1 | (1)求篮球的单价与跳绳的单价各是多少. |
| 任务2 | (2)当购买多少条跳绳时,使用方案①、方案②购买篮球和跳绳的总费用相同? |
| 任务3 | (3)若两种优惠方案可同时使用,当$ a = 60 $时,请你通过计算给出更省钱的购买方案. |
答案:
(1)设跳绳的单价是x元,则篮球的单价是$(5x+10)$元,依题意得$2(5x+10)=11x$,解得$x=20$且符合题意,所以$5x+10=5×20+10=110(\text{元})$.
答:篮球的单价是110元,跳绳的单价是20元.
(2)使用方案①购买花费$0.85(30×110+20a)=(2805+17a)$元,使用方案②购买花费$30×110+20(a-30)=(2700+20a)$元.因为要使方案①、方案②购买的总费用相同,所以$2805+17a=2700+20a$,解得$a=35$.
答:当购买35条跳绳时,使用方案①和方案②购买篮球和跳绳的总费用相同.
(3)当$a=60$时,单独使用方案①购买花费$2805+17×60=3825(\text{元})$,单独使用方案②购买花费$2700+20×60=3900(\text{元})$,先使用方案②购买30个篮球即送30条跳绳,再使用方案①单独购买30条跳绳花费$30×110+0.85×20×30=3810(\text{元})$.因为$3810<3825<3900$,所以第3种购买方案更省钱.
答:先使用方案②买30个篮球即送30条跳绳,再使用方案①单独买30条跳绳更省钱.
(1)设跳绳的单价是x元,则篮球的单价是$(5x+10)$元,依题意得$2(5x+10)=11x$,解得$x=20$且符合题意,所以$5x+10=5×20+10=110(\text{元})$.
答:篮球的单价是110元,跳绳的单价是20元.
(2)使用方案①购买花费$0.85(30×110+20a)=(2805+17a)$元,使用方案②购买花费$30×110+20(a-30)=(2700+20a)$元.因为要使方案①、方案②购买的总费用相同,所以$2805+17a=2700+20a$,解得$a=35$.
答:当购买35条跳绳时,使用方案①和方案②购买篮球和跳绳的总费用相同.
(3)当$a=60$时,单独使用方案①购买花费$2805+17×60=3825(\text{元})$,单独使用方案②购买花费$2700+20×60=3900(\text{元})$,先使用方案②购买30个篮球即送30条跳绳,再使用方案①单独购买30条跳绳花费$30×110+0.85×20×30=3810(\text{元})$.因为$3810<3825<3900$,所以第3种购买方案更省钱.
答:先使用方案②买30个篮球即送30条跳绳,再使用方案①单独买30条跳绳更省钱.
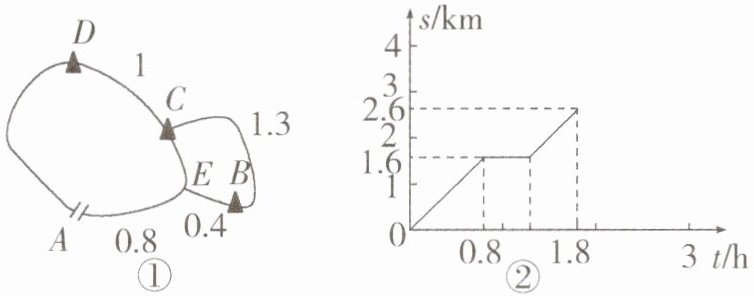
21. 某景区的旅游线路如图①所示,其中A为入口,B,C,D为风景点,E为三岔路的交汇点,图①中所给数据为相应两点间的路程(单位:km).甲游客以一定的速度沿线路“A→D→C→E→A”步行游览,在每个景点逗留的时间相同,当他回到A处时,共用去3h.甲步行的路程$ s(km) 与游览时间 t(h) $之间的部分图象如图②所示.
(1)求甲在每个景点逗留的时间,并补全图象.
(2)求C,E两点间的路程.
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候,等候时间不超过10min.如果乙的步行速度为3km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.
(1)求甲在每个景点逗留的时间,并补全图象.
(2)求C,E两点间的路程.
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候,等候时间不超过10min.如果乙的步行速度为3km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.

答案:
(1)由图②可知甲步行的速度为$\frac{1.6}{0.8}=2(\text{km/h})$,因此甲在每个景点逗留的时间为$1.8-0.8-\frac{2.6-1.6}{2}=0.5(\text{h})$,画图如下.

(2)甲步行的总时间为$3-0.5×2=2(\text{h})$.所以甲的总行程为$2×2=4(\text{km})$.所以C,E两点间的路程为$4-1.6-1-0.8=0.6(\text{km})$.
(3)他们的约定能实现.理由如下:乙游览的最短线路为$A→D→C→E→B→E→A$(或$A→E→B→E→C→D→A$),总行程为$1.6+1+0.6+0.4×2+0.8=4.8(\text{km})$.所以乙游完三个景点后回到A处的总时间为$\frac{4.8}{3}+0.5×3=3.1(\text{h})$,所以乙比甲晚6 min到达A处,所以他们的约定能实现.
(1)由图②可知甲步行的速度为$\frac{1.6}{0.8}=2(\text{km/h})$,因此甲在每个景点逗留的时间为$1.8-0.8-\frac{2.6-1.6}{2}=0.5(\text{h})$,画图如下.

(2)甲步行的总时间为$3-0.5×2=2(\text{h})$.所以甲的总行程为$2×2=4(\text{km})$.所以C,E两点间的路程为$4-1.6-1-0.8=0.6(\text{km})$.
(3)他们的约定能实现.理由如下:乙游览的最短线路为$A→D→C→E→B→E→A$(或$A→E→B→E→C→D→A$),总行程为$1.6+1+0.6+0.4×2+0.8=4.8(\text{km})$.所以乙游完三个景点后回到A处的总时间为$\frac{4.8}{3}+0.5×3=3.1(\text{h})$,所以乙比甲晚6 min到达A处,所以他们的约定能实现.
查看更多完整答案,请扫码查看


