《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

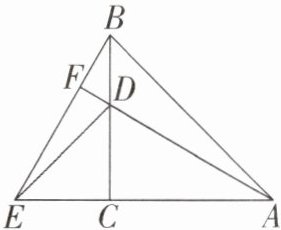
20. 把两个含有$45^{\circ }$角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.求证:$AF⊥BE$.

答案： 因为△ECD 和△BCA 都是等腰直角三角形,所以 EC=DC,BC=AC,∠ECD=∠ACB=90°.在△BEC 和△ADC 中,$\begin{cases} EC=DC, \\ ∠ECB=∠DCA, \\ BC=AC, \end{cases}$所以△BEC≌△ADC(SAS),所以∠EBC=∠DAC.因为∠DAC+∠CDA=90°,∠FDB=∠CDA,所以∠EBC+∠FDB=90°,所以∠BFD=90°,即 AF⊥BE.

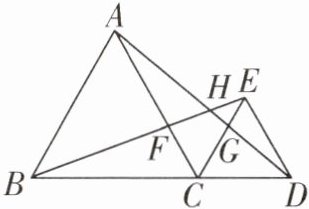
21. 如图是某部分街道公交线路示意图,BCD是直道,$AB= BC= CA,CD= DE= EC$,A,B,C,D,E,F,G,H为公共汽车停靠点,甲车从A站出发,沿$A→H→G→D→E→G→C→F$的顺序到达F站,乙车从B站出发沿$B→F→H→E→D→C→G$的顺序到达G站,如果甲、乙两车同时分别从A,B两站出发,不计各站点停靠时间,两车速度相同,问哪一辆车先到达指定站点? 为什么?

答案： 甲、乙两车同时到达指定站点.理由如下:因为 AB=BC=CA,CD=DE=EC,所以∠ACB=∠ECD=60°.所以∠ACD=∠BCE=120°.在△ACD 和△BCE 中,AC=BC,∠ACD=∠BCE,CD=CE,所以△ACD≌△BCE(SAS),所以 AD=BE,∠CBF=∠CAG.因为∠ACG=180°-60°-60°=60°,所以∠ACB=∠ACG=60°.在△ACG 和△BCF 中,∠CAG=∠CBF,AC=BC,∠ACG=∠ACB,所以△ACG≌△BCF(ASA),所以 CF=CG.因为甲车路线=AD+DE+CE+CF,乙车路线=BE+DE+CD+CG.所以甲车路线长度=乙车路线长度.因为甲、乙两车同时分别从 A,B 两站出发,两车速度相同,所以甲、乙两车同时到达指定站点.