《2025年暑假总动员宁夏人民教育出版社七年级数学北师大版》

14. 如图所示的程序计算函数值,若输入$x的值为\frac{3}{2}$,则输出的结果$y$为______.

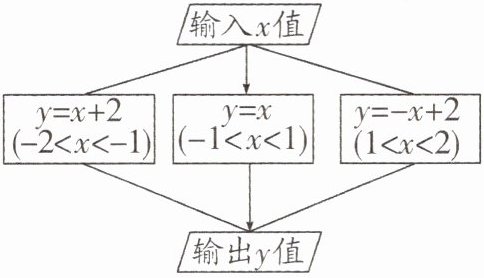
答案： 0.5

15. 如图,在$\triangle ABC$中,边$BC$长为10,$BC边上的高AD'$为6,点$D在BC$上运动,设$BD长为x(0\lt x\lt10)$,则$\triangle ACD的面积y与x$之间的关系式为______.

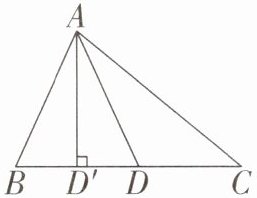
答案： y=30-3x

16. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.如图所示的图象刻画了“龟兔再次赛跑”的故事($x$表示乌龟、兔子从起点出发所行的时间,$y_{1}$表示乌龟所行的路程,$y_{2}$表示兔子所行的路程).有下列说法：
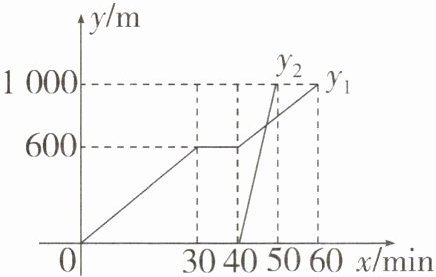
①“龟兔再次赛跑”的路程为$1000m$；②兔子和乌龟同时从起点出发；③乌龟在途中休息了$10min$.其中正确的说法是______.(把你认为正确说法的序号都填上)

答案： ①③

17. (6分)某公交车每月的支出费用为4000元,每月的乘车人数$x$(人)与每月利润(利润= 收入费用-支出费用)$y$(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的)：
|$x/$人|500|1000|1500|2000|2500|3000|…|
|$y/$元|-3000|-2000|-1000|0|1000|2000|…|
(1)在这个变化过程中,______是自变量,______是因变量.
(2)观察表中数据可知,每月乘客量达到______人以上时,该公交车才不会亏损.
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元？
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达到______人.

答案：
(1)每月的乘车人数x 每月的利润y
(2)2 000
(3)由题表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1 000元,当每月的乘车人数为2 000人时,每月利润为0元,则当每月乘车人数为3 500人时,每月利润为3 000元.
(4)4 500