第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
18. 如图,观察图形,解答问题:
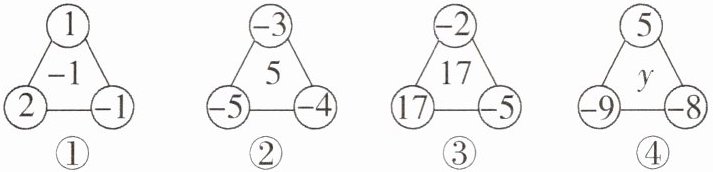
(1)按下表已填写的形式填写表中的空格;
| | 图① | 图② | 图③ |
| 三个角上三个数的积 | $ 1 × (-1) × 2 = -2 $ | $ (-3) × (-4) × (-5) = -60 $ | |
| 三个角上三个数的和 | $ 1 + (-1) + 2 = 2 $ | $ (-3) + (-4) + (-5) = -12 $ | |
| 积与和的商 | $ (-2) ÷ 2 = -1 $ | | |
(2)请用你发现的规律求出图④中的数y.

(1)按下表已填写的形式填写表中的空格;
| | 图① | 图② | 图③ |
| 三个角上三个数的积 | $ 1 × (-1) × 2 = -2 $ | $ (-3) × (-4) × (-5) = -60 $ | |
| 三个角上三个数的和 | $ 1 + (-1) + 2 = 2 $ | $ (-3) + (-4) + (-5) = -12 $ | |
| 积与和的商 | $ (-2) ÷ 2 = -1 $ | | |
(2)请用你发现的规律求出图④中的数y.
答案:
(1)图②:$(-60)÷(-12)=5$;图③:$(-2)×(-5)×17=170$,$(-2)+(-5)+17=10$,$170÷10=17$.
(2)图④:$5×(-8)×(-9)=360$,$5+(-8)+(-9)= -12$,$y=360÷(-12)=-30$.
(1)图②:$(-60)÷(-12)=5$;图③:$(-2)×(-5)×17=170$,$(-2)+(-5)+17=10$,$170÷10=17$.
(2)图④:$5×(-8)×(-9)=360$,$5+(-8)+(-9)= -12$,$y=360÷(-12)=-30$.
19. 动点H以每秒1厘米的速度沿图①的边框(边框拐角处都互相垂直)按从A-B-C-D的路径匀速运动,相应的$ \triangle HAD 的面积 S(cm^{2}) 与时间 t(s) $的关系图象如图②,已知$ AD = 4cm $,设点H的运动时间为$ t s $.

(1)图②中反映了两个变量之间的关系,其中自变量为______,因变量为______;
(2)$ BC = $______,$ a = $______,$ b = $______;
(3)当$ \triangle HAD 的面积为 8cm^{2} $时,求点H的运动时间t的值.

(1)图②中反映了两个变量之间的关系,其中自变量为______,因变量为______;
(2)$ BC = $______,$ a = $______,$ b = $______;
(3)当$ \triangle HAD 的面积为 8cm^{2} $时,求点H的运动时间t的值.
答案:
(1)点H的运动时间 △HAD的面积
(2)4 14 10
(3)当点H在BC上时,△HAD的面积为$\frac{1}{2}AD\cdot AB=\frac{1}{2}×4×5=10(\text{cm}^2)$,当△HAD的面积为$8\ \text{cm}^2$时,可分两种情况:当点H在AB上时,$S_{\triangle HAD}=\frac{1}{2}AD\cdot AH=8\ \text{cm}^2$,则$AH=4\ \text{cm}$,所以$t=4÷1=4\ (\text{s})$,当点H在CD上时,$S_{\triangle HAD}=\frac{1}{2}AD\cdot DH=8\ \text{cm}^2$,则$DH=4\ \text{cm}$,所以$t=(5+4+5-4)÷1=10(\text{s})$.综上,当△HAD的面积为$8\ \text{cm}^2$时,点H的运动时间t的值为4或10.
(1)点H的运动时间 △HAD的面积
(2)4 14 10
(3)当点H在BC上时,△HAD的面积为$\frac{1}{2}AD\cdot AB=\frac{1}{2}×4×5=10(\text{cm}^2)$,当△HAD的面积为$8\ \text{cm}^2$时,可分两种情况:当点H在AB上时,$S_{\triangle HAD}=\frac{1}{2}AD\cdot AH=8\ \text{cm}^2$,则$AH=4\ \text{cm}$,所以$t=4÷1=4\ (\text{s})$,当点H在CD上时,$S_{\triangle HAD}=\frac{1}{2}AD\cdot DH=8\ \text{cm}^2$,则$DH=4\ \text{cm}$,所以$t=(5+4+5-4)÷1=10(\text{s})$.综上,当△HAD的面积为$8\ \text{cm}^2$时,点H的运动时间t的值为4或10.
查看更多完整答案,请扫码查看


