《2025年名师帮同步学案九年级数学全一册人教版》

1. 弧长公式：$l=\frac {n\cdot 2πR}{360}=$$\frac{n\pi R}{180}$.(其中n为圆心角的度数，R为圆的半径)
①在弧长的计算公式中，n是表示$1^{\circ }$的圆心角的倍数，n和180都不要带单位；
②若圆心角的单位不全是度，则需要先化为度后再计算弧长；
③题设未标明精确度的，可以将弧长用π表示.

答案： $\frac{n\pi R}{180}$

2. 度数相等的弧，弧长不一定相等，弧长相等的弧不一定是等弧.(均填“一定”或“不一定”)

答案： 不一定　不一定

1. 在半径为6cm的圆中，$60^{\circ }$圆心角所对的弧长为$2\pi$cm.（结果保留π）

答案： $2\pi$

2. 扇形的半径是9cm，弧长是3πcm，则此扇形的圆心角为60度.

答案： 60

3. 已知扇形的圆心角为$45^{\circ }$，弧长等于$\frac {π}{2}$，则该扇形的半径为______2.

答案： 2 解析:根据弧长的公式 $l=\frac{n\pi R}{180}$，知 $R=\frac{180l}{n\pi}=\frac{180×\frac{\pi}{2}}{45\pi}=2$，即该扇形的半径为 2.

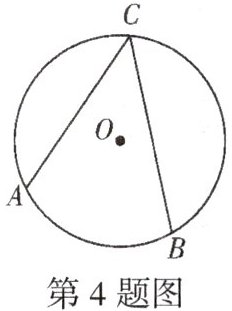
4. 如图，点A，B，C是半径为4的$\odot O$上的三点.如果$∠ACB=45^{\circ }$，那么$\overset{\frown }{AB}$的长为 （B）

A. π
B. 2π
C. 3π
D. 4π

答案： B

5.（2025·长沙一模）如图，将$\triangle ABC$绕点O逆时针旋转$60^{\circ }$至$\triangle COD$，若$OA=3$，则点A旋转到点C所经过的路径长为$\pi$.

答案： $\pi$

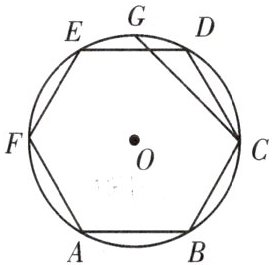
6. 如图，已知六边形ABCDEF是$\odot O$的内接正六边形，点G是$\overset{\frown }{DE}$的中点.若$\odot O$的半径为6，求$\overset{\frown }{CG}$的长.

答案：
解:如图,连接 $OC$，$OD$，$OG$，$OE$，

∵ 正六边形 $ABCDEF$ 内接于 $\odot O$，
∴ $\angle COD=\angle DOE=60^{\circ}$，
∵ 点 $G$ 是 $\overset{\frown}{DE}$ 的中点，
∴ $\angle DOG=\frac{1}{2}\angle DOE=30^{\circ}$，
∴ $\angle COG=90^{\circ}$，
∵ $\odot O$ 的半径为 6，
∴ $\overset{\frown}{CG}$ 的长为 $\frac{90\pi×6}{180}=3\pi$.